Mass Matrix Computation in the Finite Element Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
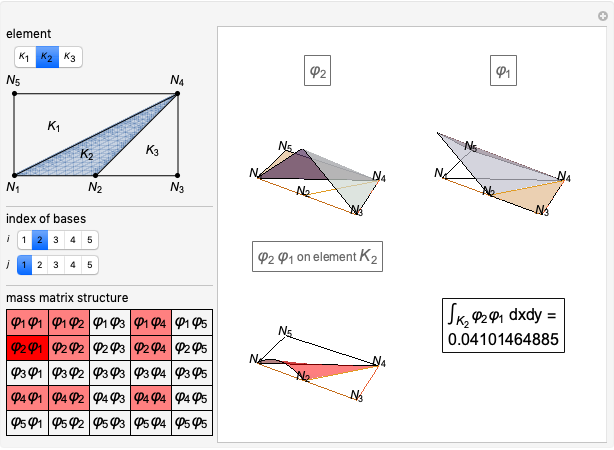
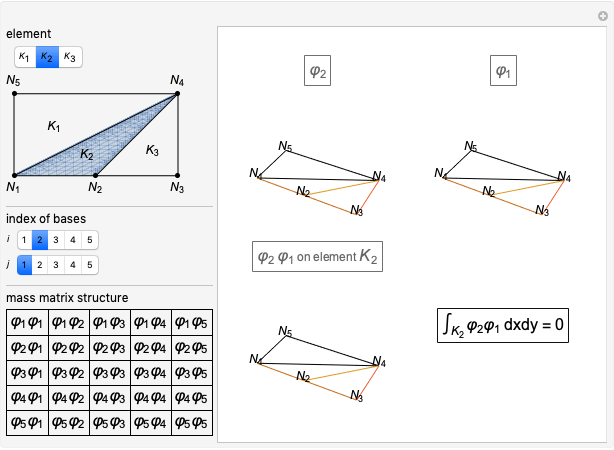
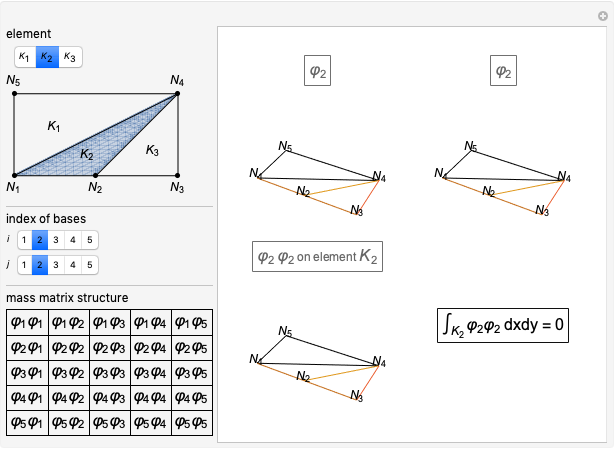
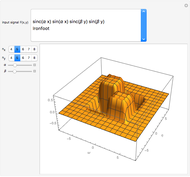
This Demonstration shows the computation of the mass matrix in a particular example of the finite element method. It considers piecewise linear basis functions. You can explore all the cross products of basis functions elementwise in a very simple mesh.
Contributed by: Mikel Landajuela (July 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
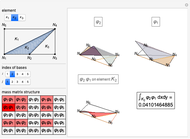
Consider the rectangular domain 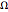 and the finite-element mesh composed of five nodes
and the finite-element mesh composed of five nodes 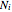 and three elements
and three elements 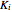 as shown in the top-left part of the results.
as shown in the top-left part of the results.
The five piecewise linear basis functions 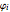 associated to each of the nodes
associated to each of the nodes 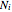 are shown in the results.
are shown in the results.
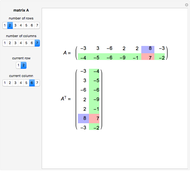
The mass matrix is defined as
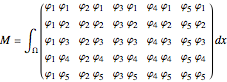 .
.
The finite element approximation reads: Find 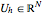 such that
such that 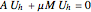 , where
, where 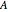 is the stiffness matrix (
is the stiffness matrix (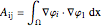 ) and
) and 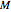 is the mass matrix.
is the mass matrix.
In finite-element programming, the computation of this matrix is usually performed elementwise, looping over all the elements and adding the nonzero contributions to the global matrix:

Many of the matrix elements are zero, so that 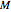 reduces to:
reduces to:
 .
.
References
[1] M. G. Larson and F. Bengzon, The Finite Element Method: Theory, Implementation, and Applications, Springer-Verlag: Berlin, Heidelberg, 2013.
[2] A. Ern and J.-L. Guermond, Theory and Practice of Finite Elements, Springer-Verlag: New York, 2004.
Permanent Citation