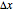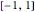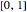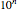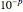Solving Matrix Systems with Real, Interval, or Uncertain Elements

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
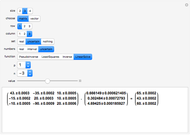
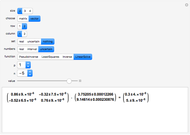
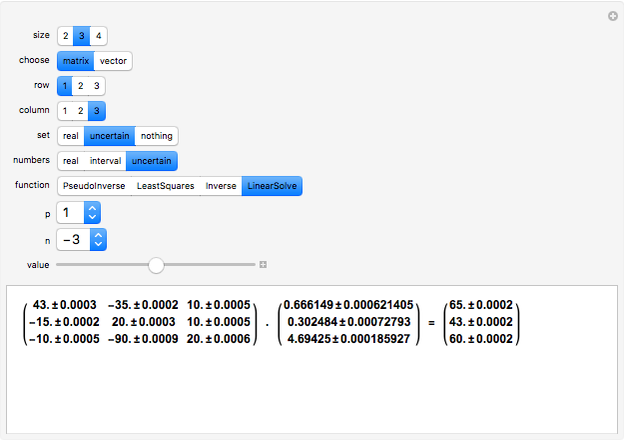
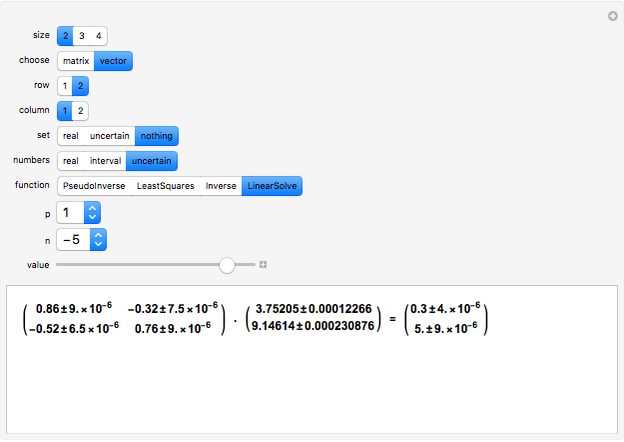
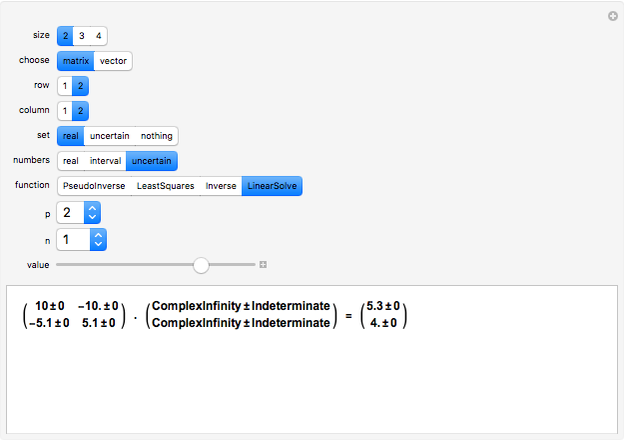
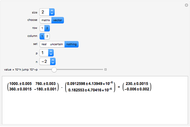
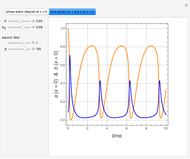
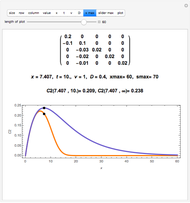
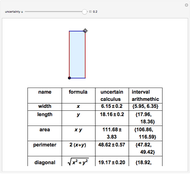
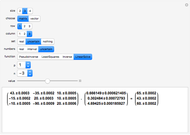
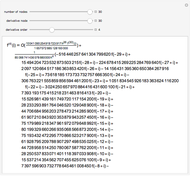
This Demonstration solves the system of linear equations given in the pane. Its size can be 2, 3, or 4. Set the elements (the real and uncertain parts) of the matrix and the right‐hand side (rhs) vector for all the rows and columns by using the "value" slider.
[more]
Contributed by: Valter Yoshihiko Aibe and Mikhail Dimitrov Mikhailov (March 2011)
Open content licensed under CC BY-NC-SA
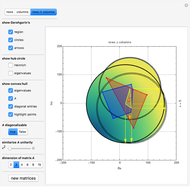
Snapshots
Details
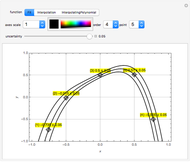
The solution vector is dynamically updated by one of the Mathematica built-in functions PseudoInverse, LeastSquares, Inverse, or LinearSolve. It is desirable to use PseudoInverse or LeastSquares when setting the matrix and vector elements. Once the desired matrix and rhs vector are fixed, you can compare the solutions given by all four built-in functions for real, interval, and uncertain numbers.
There is international consensus on the evaluation of standard uncertainty and combined standard uncertainty in measurement and computations [1, 2]. Just as the International System of Units (SI) has brought coherence to all scientific and technological measurements, the worldwide consensus on uncertainty permits a vast spectrum of results to be readily understood and properly interpreted. The needs of numerous testing laboratories to calculate the measurement uncertainty on a large scale is supported by numerous software tools. Rasmussen [3] refers to 10 different software packages.
To facilitate the calculation of the combined standard uncertainty similar to complex and interval numbers, Aibe and Mikhailov introduced a new object 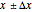 called an uncertain number [4] and developed in Mathematica 6 an Uncertain Calculus package transforming any functional relationship of uncertain numbers
called an uncertain number [4] and developed in Mathematica 6 an Uncertain Calculus package transforming any functional relationship of uncertain numbers 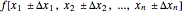 into an uncertain number
into an uncertain number 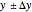 , assuming that all arguments of the function
, assuming that all arguments of the function 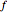 are independent. The rules manipulating uncertain numbers in this Demonstration are extracted from the Uncertain Calculus package [4].
are independent. The rules manipulating uncertain numbers in this Demonstration are extracted from the Uncertain Calculus package [4].
This Demonstration solves a system of linear equations 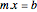 , where
, where  is a vector of variables and
is a vector of variables and  and
and  are a matrix and a vector with real, interval, and uncertain elements. The real and interval numbers are obtained from the uncertain numbers.
are a matrix and a vector with real, interval, and uncertain elements. The real and interval numbers are obtained from the uncertain numbers.
The elements of the initialization diagonal matrix and vector are uncertain numbers 1±0. The "size" of the system is limited to four equations in order to show the entire matrix dot multiplied by the solution vector and the rhs vector. The uncertainty of elements changes only the uncertainty of the solution.
When the matrix has a nonzero determinant, then the built-in functions Inverse and LinearSolve find the unique solution. However, if the determinant is zero (the matrix is singular) there may be either no vector or an infinite number of vectors satisfying the system. Nevertheless, for a singular matrix the built-in functions PseudoInverse or LeastSquares give solutions that minimize the sum of the squares of all entries in  ·Inverse[
·Inverse[ ]-
]-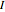 , where
, where 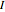 is the identity matrix. The Demonstration lets you compare the uncertainty introduced by all four of these built‐in functions.
is the identity matrix. The Demonstration lets you compare the uncertainty introduced by all four of these built‐in functions.
In the authors' experiments, Inverse surprisingly introduces less uncertainty than LinearSolve, while PseudoInverse and LeastSquares introduce the highest uncertainty.
References:
[1] European Cooperation for Accreditation of Laboratories, Expression of the Uncertainty of Measurement in Calibration, EAL-R2 and EAL-R2-S1, 1997.
[2] International Organization for Standardization, Guide to the Expression of Uncertainty in Measurement, Geneva, Switzerland: ISO, 1995.
[3] S. N. Rasmussen, "Software Tools for the Expression of Uncertainty in Measurement," MetroTrade Workshop on Traceability and Measurement Uncertainty in Testing, Berlin, January 30–31, 2003.
[4] V. Y. Aibe and M. D. Mikhailov, "Uncertainty Calculus in Metrology," Proceedings of ENCIT 2008, 12th Brazilian Congress of Thermal Engineering and Sciences, Belo Horizonte, MG, Brazil, November 10–14, 2008.
Permanent Citation