Mass Transfer in Binary Star Systems

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
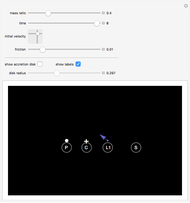
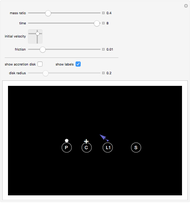
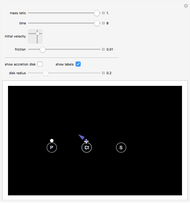
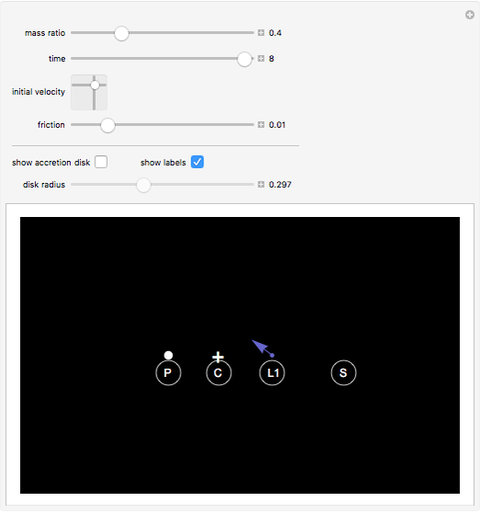
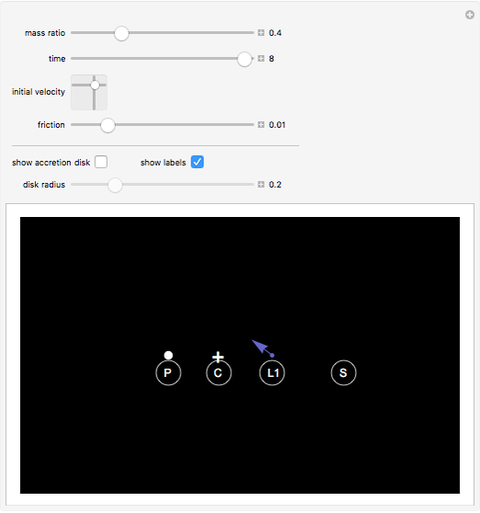
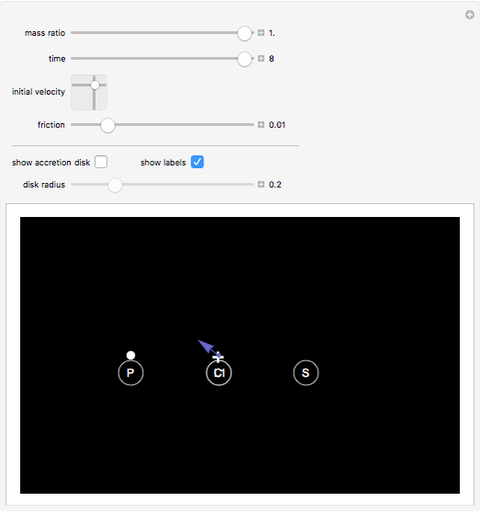
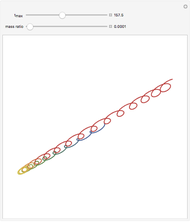
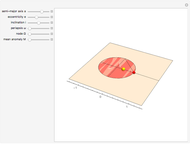
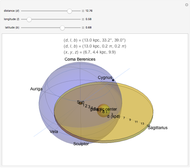
This Demonstration shows the path of a gas particle transferred from a secondary star (S) to a more massive primary star (P) in a binary star system. The gas particle starts at the first Lagrange point (L1). The mass ratio is the ratio of the masses S to P. The initial velocity is shown as a blue arrow and the center of mass (C) is at the point marked +.
[more]
Contributed by: Jeff Bryant (March 2011)
Additional contributions by: Waylena McCully
Open content licensed under CC BY-NC-SA
Snapshots
Details
mass ratio — the ratio of the masses of the mass-losing secondary star to the mass-gaining primary star
time — the number of elapsed orbits of the binary star system
initial velocity — The  component is the component of the initial velocity of the particle in the direction of the mass-gaining primary star. The
component is the component of the initial velocity of the particle in the direction of the mass-gaining primary star. The 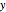 component is the component of the initial velocity of the particle in the direction of the orbit of the mass-losing star (in this simulation, the direction is up)
component is the component of the initial velocity of the particle in the direction of the orbit of the mass-losing star (in this simulation, the direction is up)
friction — the coefficient that governs the orbital decay of the transfer particle
In a binary system, the first Lagrange point (L1) is the point of gravitational equilibrium between the two stars. When the secondary star grows so large that L1 is on its surface, gas transfers from that point to the more massive primary star. This type of system is also known as a semi-detached binary star system. The path of a particle of gas depends on its initial velocity and the friction caused by other gas particles in the transfer.
Snapshot 1: This shows the trajectory of the mass transfer stream with low friction.
Snapshot 2: The masses of the stars are equal, so the center of mass is at the first Lagrange point.
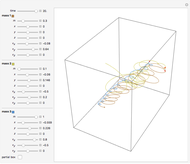
Snapshot 3: With high friction, the trajectory steadily decays.
Permanent Citation
"Mass Transfer in Binary Star Systems"
http://demonstrations.wolfram.com/MassTransferInBinaryStarSystems/
Wolfram Demonstrations Project
Published: March 7 2011