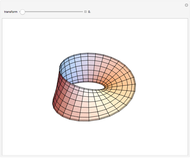
Möbius Strip as a Half-Twisted Square Torus
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
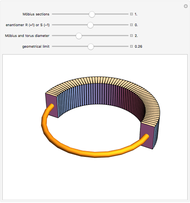
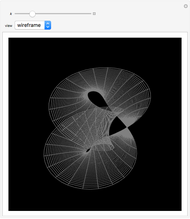
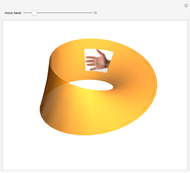
The square half-twisted torus can be changed into a Möbius strip if you shrink the square to a line segment, and vice versa. You can also change chirality to observe the isomers becoming mirror images of each other.
Contributed by: V. M. Chapela and M. J. Percino (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
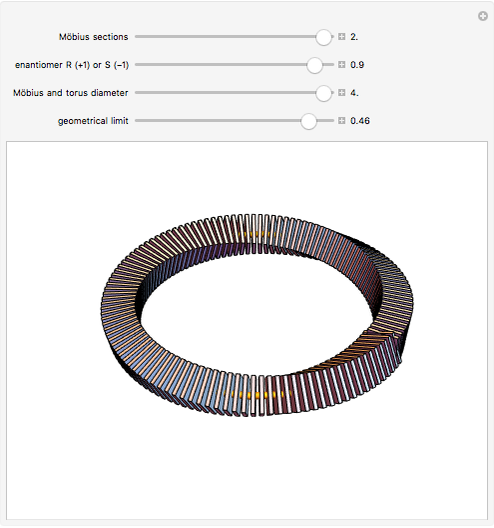
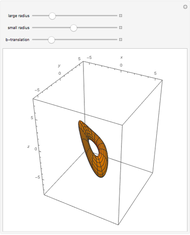
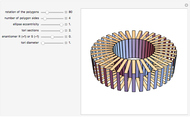
There are four sliders:
1. Möbius sections
2. enantiomer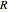 
(+1) or 
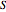(-1)
3. Möbius and torus diameter
4. geometrical limit
The first slider makes the Möbius sections grow from 0 to 360 degrees. The Möbius strip is constructed from a large number of discrete cuboids that are rotated about a circle. This is similar to the torus, a surface of revolution generated by revolving a circle in three dimensions about an axis perpendicular to the circle.
The second slider, enantiome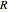r or 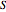, changes the twist.
The third slider makes the Möbius strip and squared section diameter larger or smaller.
The fourth slider increases or decreases the rectangular pieces from a flat plate to a square cross section.
For more information, visit the following website:
Permanent Citation
Associated Surface of a Minimal Möbius Strip
Enrique Zeleny
A Family of Surfaces Including a Möbius Strip
Ali Naeemi
Wente Torus
Enrique Zeleny
Hand Moving on a Moebius Strip
Enrique Zeleny
Seven-Coloring of a Torus
Izidor Hafner
Torus in Nil-Space
Benedek Schultz and János Pallagi
Chart for a Torus
Aaron T. Becker and Haoran Zhao
Motion Traced on the Torus and Klein Bottle
Kevin Sonnanburg
Morphing a Möbius Strip into a Torus
Oliver Seipel
Möbius Strip Made from a Rotating Bar
Sándor Kabai
