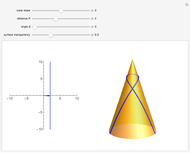
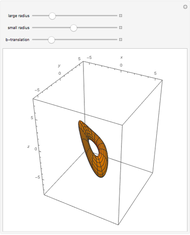
Torus in Nil-Space

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
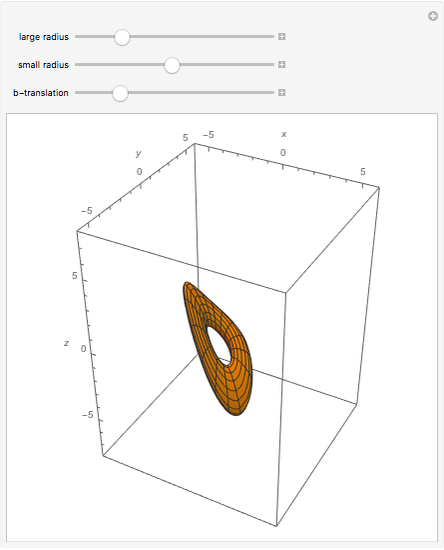
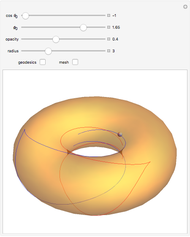
W. Heisenberg's real matrix group provides a noncommutative translation group of an affine three-space. The Nil-geometry, which is one of the eight Thurston three-geometries, can be derived from this group. E. Molnár proved that the homogeneous three-spaces have a unified interpretation in the projective three-sphere 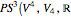 ). Here, the tori of the Nil-space are visualized.
). Here, the tori of the Nil-space are visualized.
Contributed by: Benedek Schultz and János Pallagi (June 2009)
Suggested by: Jenő Szirmai
Open content licensed under CC BY-NC-SA
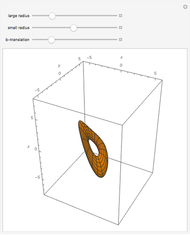
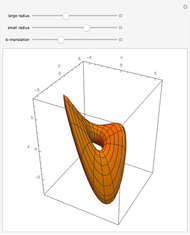
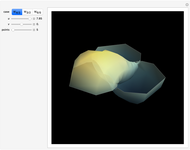
Snapshots
Details
By creating an intersection of an origin-centered geodesic ball with the  -
- plane in the Nil-space we get a geodesic sphere lying in
plane in the Nil-space we get a geodesic sphere lying in  -
- plane.
plane.
If 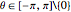 ,
,
 ,
,
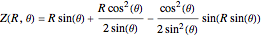 ;
if
;
if 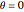 ,
,  ,
,  .
.
Now on this intersection we can use a translation defined by right multiplication by Heisenberg's matrix:
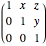
 =
= 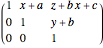 .
.
In the case  , this is the ordinary Euclidean translation in the
, this is the ordinary Euclidean translation in the  -
- plane.
plane.
Finally, we rotate the sphere around the  axis with the following as
axis with the following as 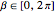 :
:
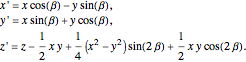
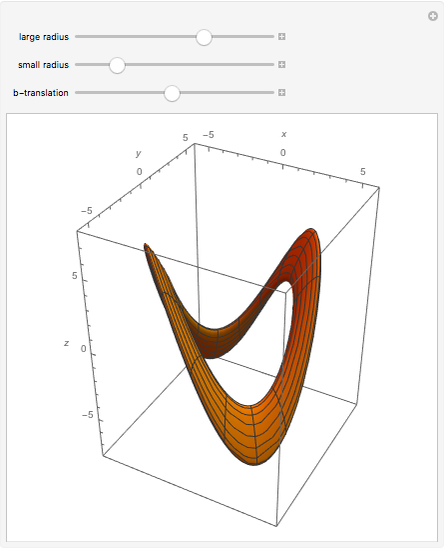
As we can see the  -translation changes the shape of the torus.
-translation changes the shape of the torus.
Reference:
J. Szirmai, "The Densest Geodesic Ball Packing by a Type of Nil Lattices," Beiträge zur Algebra und Geometrie (Contributions to Algebra and Geometry), 48(2), 2007 pp. 383–397.
Permanent Citation