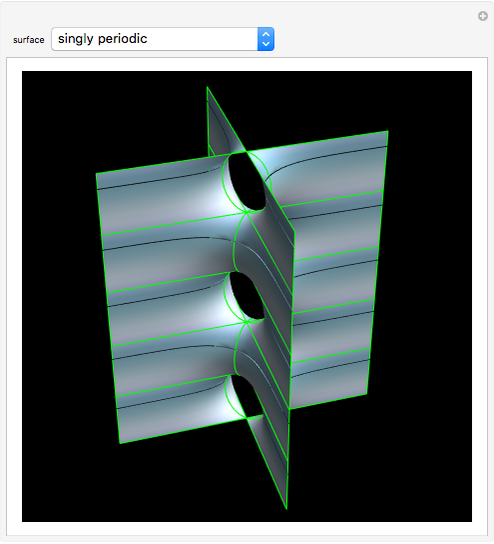
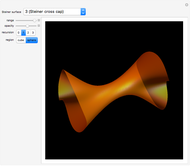
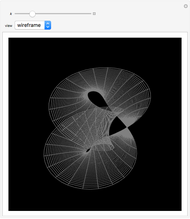
Wente Torus

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
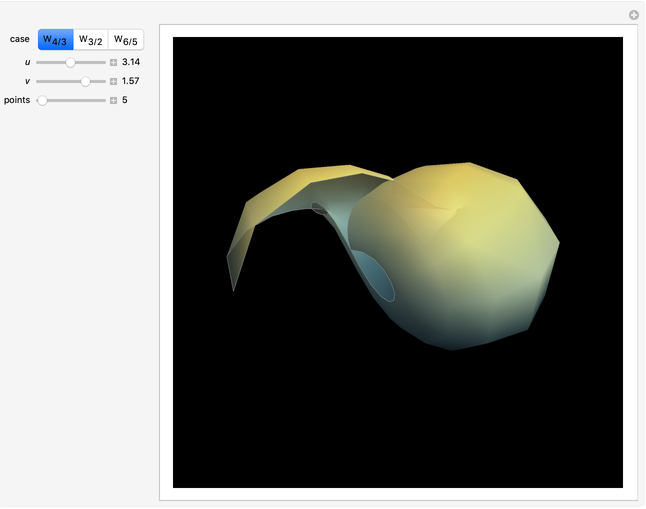
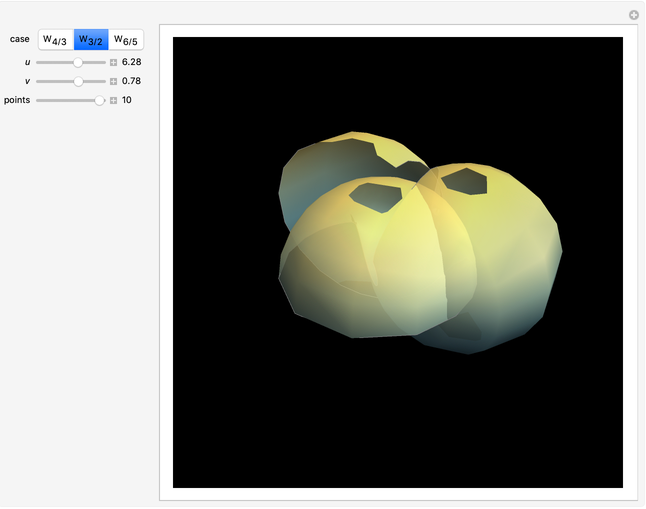
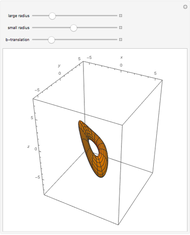
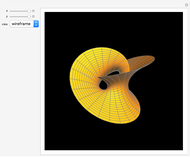
In 1894, Henry Wente discovered the Wente torus, an immersed torus of constant (but not zero) mean curvature. Such constant mean curvature (CMC) surfaces are counterexamples to Hopf's conjecture that a sphere is the only closed surface with constant mean curvature that is compact [1]. The set of all symmetric tori is in one-to-one correspondence with the set of reduced fractions 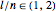 ; each
; each  corresponds to a symmetric Wente torus labeled as
corresponds to a symmetric Wente torus labeled as 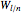 [2].
[2].
Contributed by: Enrique Zeleny (June 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] H. C. Wente, "Counterexample to a Conjecture of H. Hopf," Pacific Journal of Mathematics, 121(1), 1986 pp. 193–243. projecteuclid.org/euclid.pjm/1102702809.
[2] Marija Ćirić, "Notes on Constant Mean Curvature Surfaces and Their Graphical Presentation," Filomat 23(2), 2009 pp. 97–107. www.pmf.ni.ac.rs/pmf/publikacije/filomat/2009/23-2-2009/Paper10.pdf.
[3] M. Heil. CMC: Pictures of Constant Mean Curvature Tori [Video]. (Jun 16, 2014) www.youtube.com/watch?v=7rnsdcS7qGU.
Permanent Citation