Natural Logarithm Approximated by Continued Fractions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
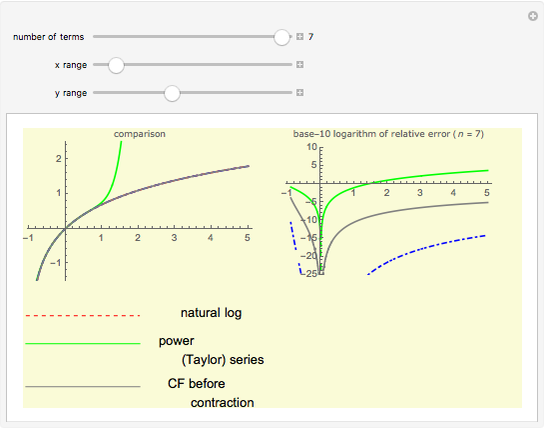
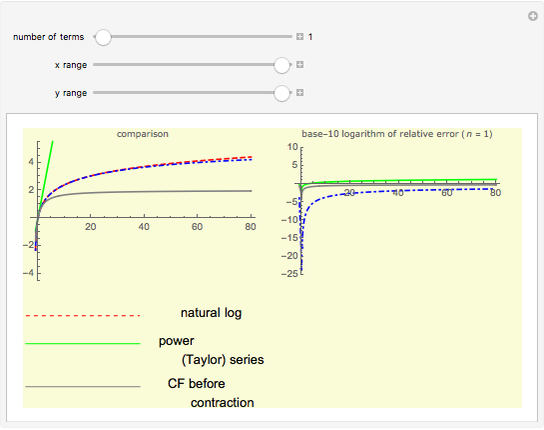
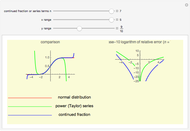
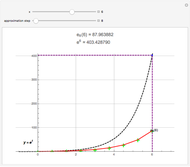
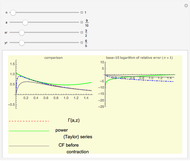
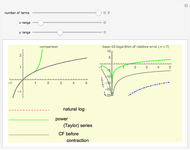
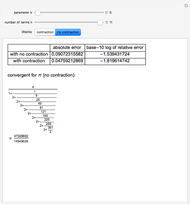
Continued fractions provide a very effective toolset for approximating functions. Usually the continued fraction expansion of a function approximates the function better than its Taylor or Fourier series. This Demonstration compares the quality of three approximations to 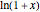 . One is the Taylor series and the other two are continued fraction expansions. The first continued fraction expansion can be obtained as a canonical even contraction of a continued fraction using Euler's method to transform a series to an
. One is the Taylor series and the other two are continued fraction expansions. The first continued fraction expansion can be obtained as a canonical even contraction of a continued fraction using Euler's method to transform a series to an 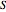 -fraction. The other continued fraction expansion was developed by the author as a canonical even contraction from the first one.
-fraction. The other continued fraction expansion was developed by the author as a canonical even contraction from the first one.
Contributed by: Andreas Lauschke (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Vary the number of terms used in the expansions to see that the Taylor series makes hardly any progress. The terms in the Taylor polynomial become progressively more complicated; higher terms have huge numbers in the numerator, the denominator, and the exponent, but the contribution of this "expense" becomes quite stale. In fact, in the base-10 log plot the green curve is mostly above the  axis.
axis.
The continued fraction expansion approximates the natural logarithm by several orders of magnitude better, as can be seen in the log-plot of the relative errors. It is generally a shortcoming of polynomials that for large 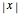 they cannot approximate functions well that converge to constants or do not have zeros, as polynomials tend to
they cannot approximate functions well that converge to constants or do not have zeros, as polynomials tend to 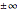 for large
for large 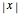 . Rational function approximation—for example continued fractions or Padé approximations—or certain special functions are much better.
. Rational function approximation—for example continued fractions or Padé approximations—or certain special functions are much better.
The original continued fraction is
 .
.
The continued fraction resulting from the author's canonical even contraction (using HornerForm for all polynomials) is
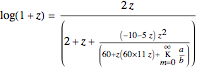 ,
,
with

and
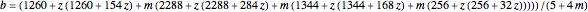 .
.
Additional Information:
The algorithm uses the backward recurrence method to compute the continued fraction expansion. This method has been shown to be extremely stable for most continued fraction expansions, which is extremely important on numerical platforms that incur truncation/round-off error due to the limitations of machine precision. It can be shown that the backward recurrence method ("from tail to head") is vastly more stable (even self-correcting) than the forward recurrence method ("from head to tail") for two important classes of continued fractions: the Stieltjes continued fractions (which includes the 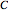 -fractions) and those that fulfill the parabolic convergence region theorem. Several function classes with known Stieltjes continued fraction expansions include: exponential integrals, incomplete gamma functions, logarithms of gamma functions, the error function, ratios of successive Bessel functions of the first kind, Euler's hypergeometric function, as well as various elementary transcendental functions. The forward recurrence method (which solves a second-order linear difference equation), however, can be computationally more efficient due to the carry-over of results from one step to the next, which is a property the backward recurrence method does not possess.
-fractions) and those that fulfill the parabolic convergence region theorem. Several function classes with known Stieltjes continued fraction expansions include: exponential integrals, incomplete gamma functions, logarithms of gamma functions, the error function, ratios of successive Bessel functions of the first kind, Euler's hypergeometric function, as well as various elementary transcendental functions. The forward recurrence method (which solves a second-order linear difference equation), however, can be computationally more efficient due to the carry-over of results from one step to the next, which is a property the backward recurrence method does not possess.
The backward recurrence method of the continued fraction expansion is also more stable than its conversion to a Padé approximation (even when several forms of the Horner form of the numerator and denominator polynomials are used), which is very important on strictly numerical platforms.
Permanent Citation