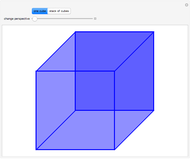
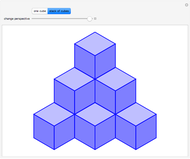
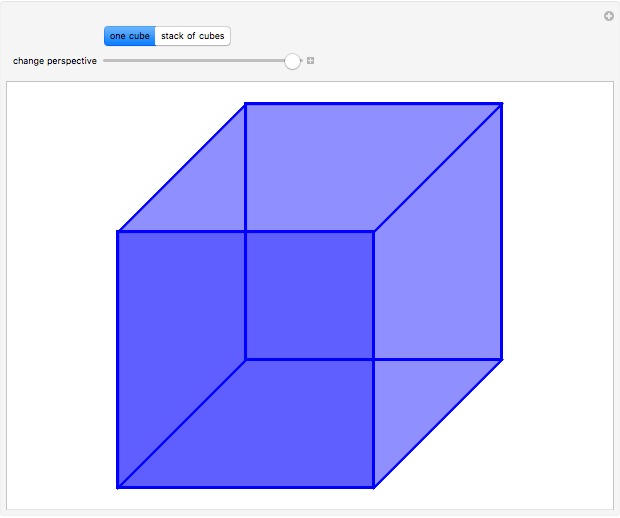
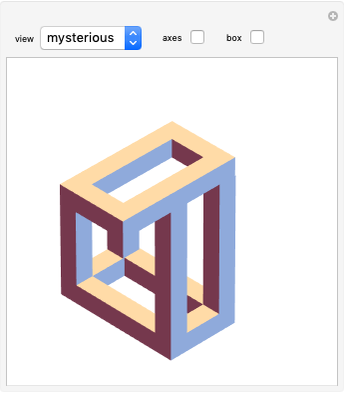
The Necker cube is an optical illusion showing a two-dimensional line drawing of a cube in which it is ambiguous which of the two squares represents the front and back surfaces from the perspective of the viewer. Alternatively, it is ambiguous which of the two rhombi represents the top or bottom of the cube. An observer staring at the figure will usually experience a sensory oscillation between the two viewpoints. The figure was first published in 1832 by the Swiss crystallographer Louis Albert Necker.