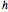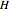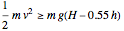Olympic Pole Vaulting

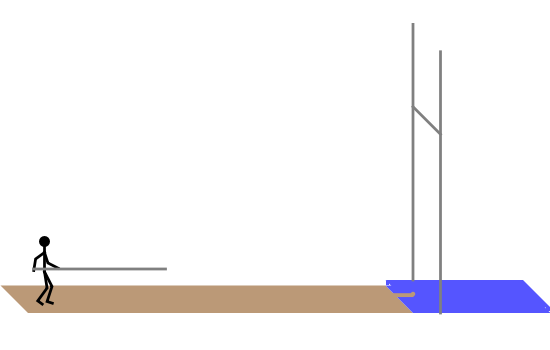
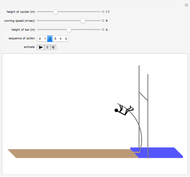
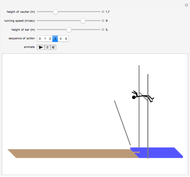
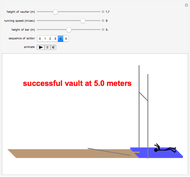
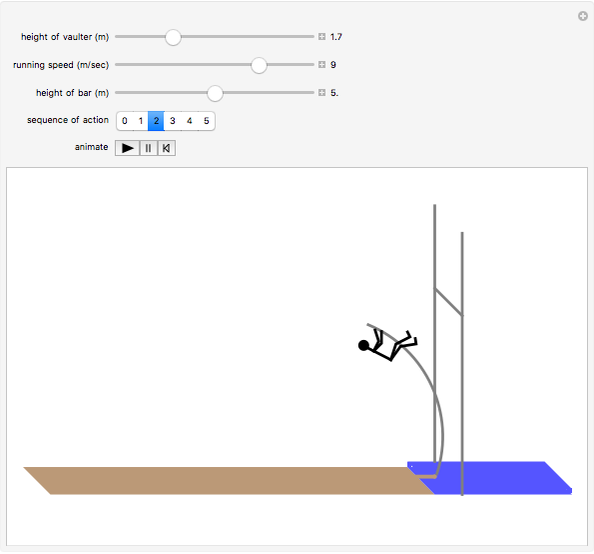
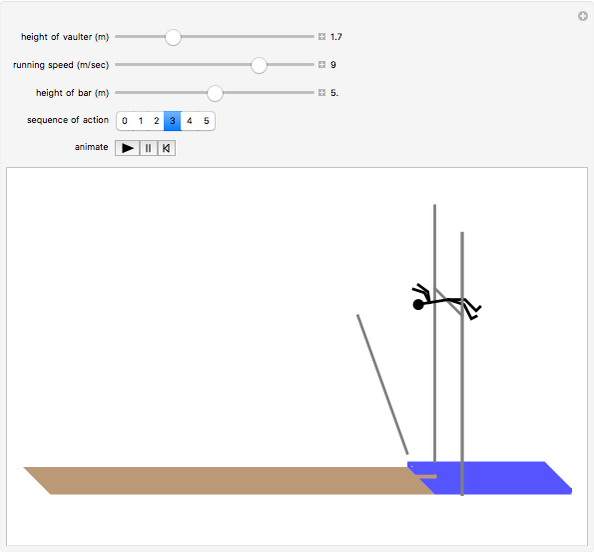
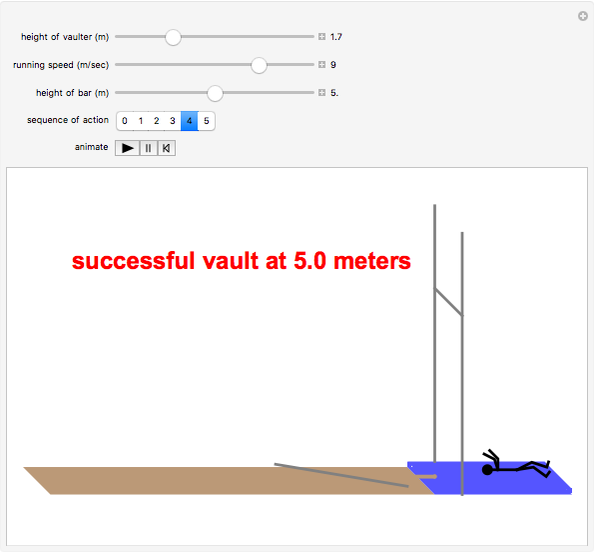
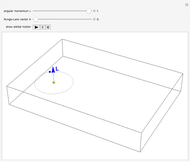
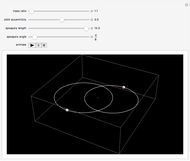
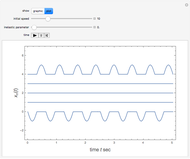
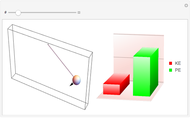
The pole vault is an Olympic event that demands a very high level of athletic ability. Nevertheless, it illustrates very simply the law of conservation of energy. The vaulter tries to achieve maximum kinetic energy by sprinting down the runway. At the end of the approach, the flexible fiberglass pole is planted in the box at the base of the pit. The kinetic energy gained in the sprint is converted into potential energy stored by elastic deformation of the pole. This, in turn, is converted into gravitational potential energy as the vaulter attempts to clear the crossbar.

For a person with a height of meters, the body's center of gravity is estimated to be at 0.55. Suppose the athlete can achieve a maximum speed of meters/second (world-class sprinters can do 10 m/sec). For the center of gravity to successfully reach the height of the crossbar, the energy relation must be satisfied, where is the acceleration of gravity, 9.81 m/sec. This result assumes perfect technique as well as 100% efficient conversion of energy at each stage. The effects of wind resistance, crowd noise, and other distractions are neglected. Likewise neglected is the possibility of additional lift achieved by pushing down on the pole just before release.

The above energy relation has been found to be remarkably accurate. The world's record pole vault was set by Sergei Bubka (USSR/Ukraine) with a 6.15-meter pole vault. Only 15 men have achieved the 6-meter mark. The women's record is just over 5 meters.