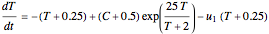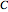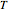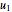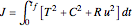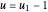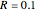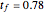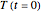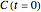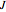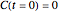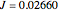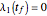Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Optimal Control of a Continuous Stirred-Tank Reactor

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

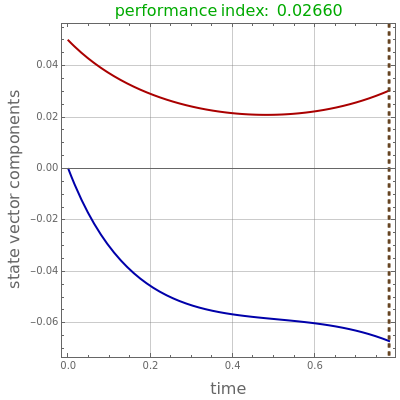
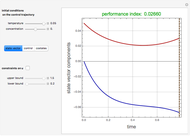
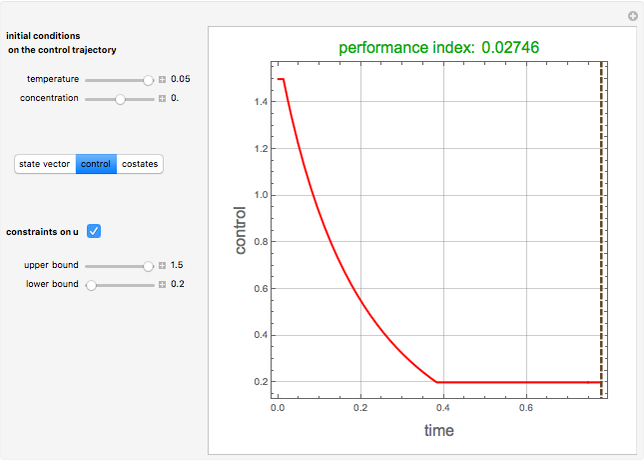
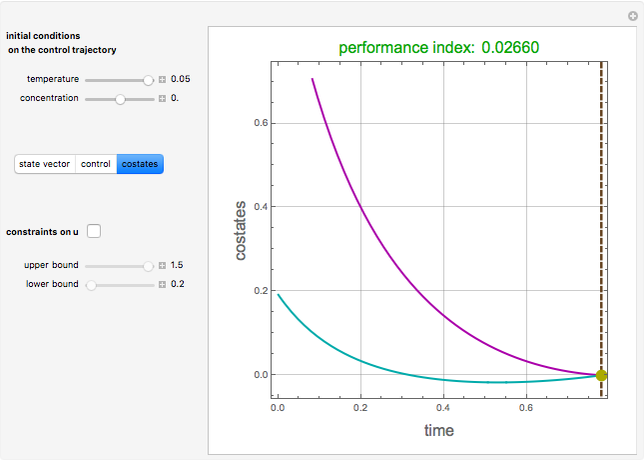
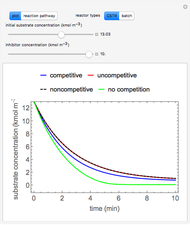
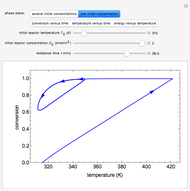
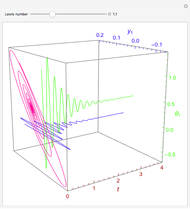
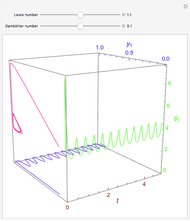
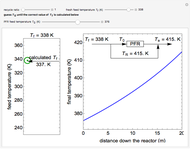
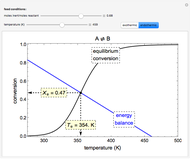
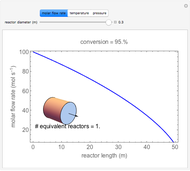
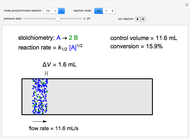
Aris and Amundson [1–3] originally analyzed the design of a continuous stirred-tank reactor (CSTR) with a first-order, irreversible exothermic reaction. The reactor is controlled by varying the flow of a cooling fluid through a coil inside the reactor. The state equations for the CSTR are given by

[more]

,

,

where and are the deviations from steady-state concentration and temperature, respectively, and is the control action.

This Demonstration finds the optimal control, which minimizes the performance index given by , where the normalized control action is and is a weighting parameter. Assume a final time of the control [4, 5]. You can set the initial conditions (i.e. both and ) and choose to apply upper and lower bounds on .

We plot the component of the state vector ( and shown in red and blue, respectively), the normalized control , and the costates. We also compute the value of the performance index .

For the case where is unbounded, if you select the initial conditions and , then , in close agreement with the result found in [4] and [5].

The costates and are plotted in magenta and cyan. The costates verify and (yellow dot).

[less]

Contributed by: Housam Binous and Ahmed Bellagi (January 2016)
(King Fahd University of Petroleum & Minerals, KSA; University of Monastir, Tunisia)
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] R. Aris and N. R. Amundson, "An Analysis of Chemical Reactor Stability and Control—I: The Possibility of Local Control, with Perfect or Imperfect Control Mechanisms," Chemical Engineering Science, 7(3), 1958 pp. 121–131. doi:10.1016/0009-2509(58)80019-6.

[2] R. Aris and N. R. Amundson, "An Analysis of Chemical Reactor Stability and Control—II: The Evolution of Proportional Control", Chemical Engineering Science, 7(3), 1958 pp. 132–147. doi:10.1016/0009-2509(58)80020-2.

[3] R. Aris and N. R. Amundson, "An Analysis of Chemical Reactor Stability and Control—III: The Principles of Programming Reactor Calculations. Some Extensions", Chemical Engineering Science, 7(3), 1958 pp. 148–155. doi:10.1016/0009-2509(58)80021-4.

[4] R. Luus and L. Lapidus, "The Control of Nonlinear Systems. Part II: Convergence by Combined First and Second Variations," AIChE Journal, 13(1), 1967 pp. 108–113. doi:10.1002/aic.690130120.

[5] D. E. Kirk, Optimal Control Theory: An Introduction, Mineola, NY: Dover Publications, 2004.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send