Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

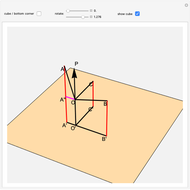
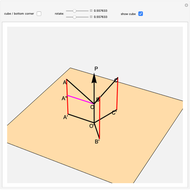
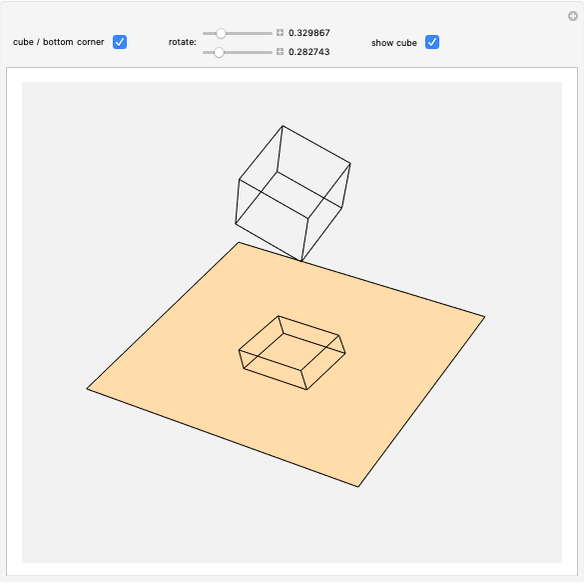
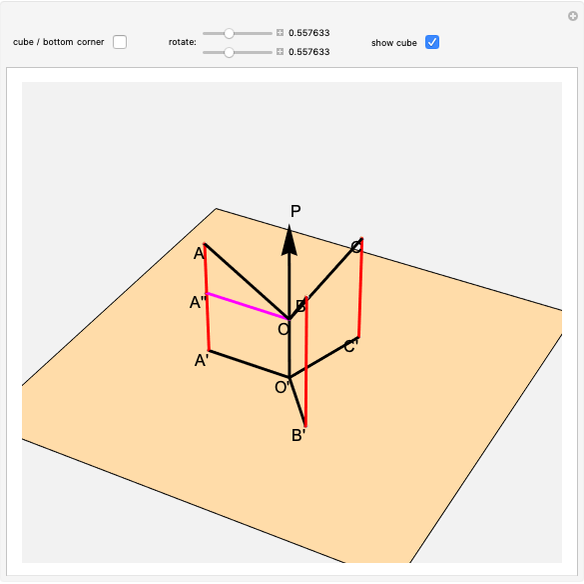
Orthogonal Projections of the Edges of a Cube

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

This Demonstration shows that the sum of the squares of the lengths of the orthogonal projections of the edges of a cube with edge length to a plane equals .

[more]

Let the bottom corner of the cube (a trihedron) have bottom vertex and three sides , , of length . Let be perpendicular to with . Let the angles of to the three sides be , , . Take the trihedron as the axes of a coordinate system with . Then , , , and so [1, p.27].

The length of the projection of to is , and similarly for and . So the lengths of the projections of the three edges are , , . Now

.

The 12 edges of the cube are parallel in sets of four, so the sum of the squares of all the edge lengths equals .

[less]

Contributed by: Izidor Hafner (May 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

This problem was posed in [1, pp. 20, 27, 28].

Reference

[1] V. V. Prasolov and I. F. Sharygin, Problems in Stereometry (in Russian), Moscow: Nauka, 1989.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send