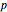Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Parliamentary Seat Allocation by the Sainte-Laguë Method

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

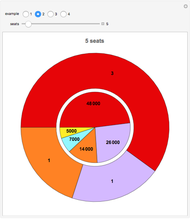
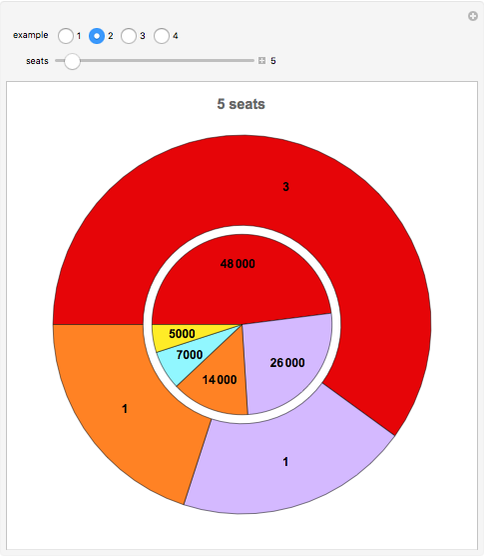
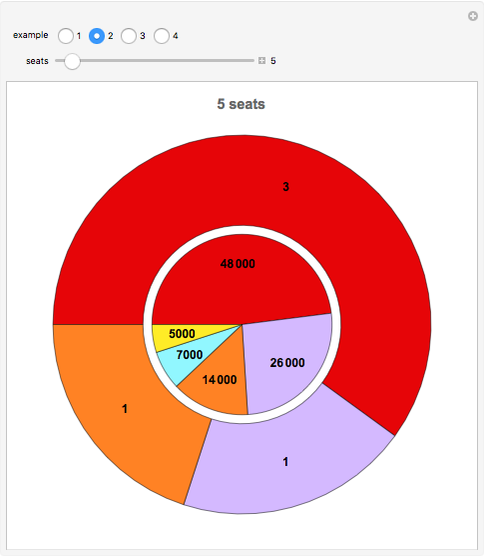
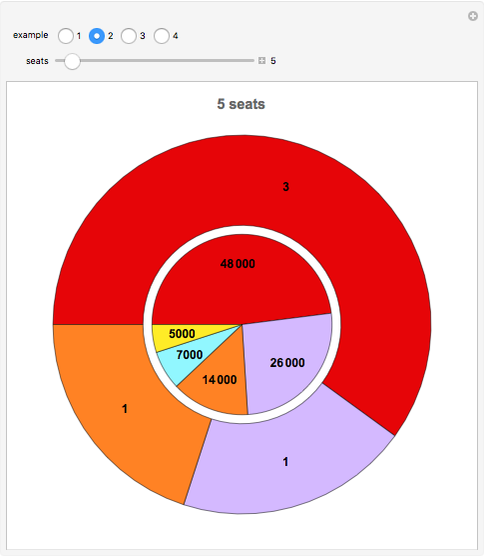
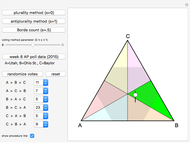
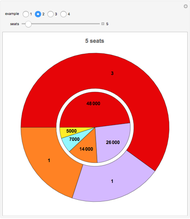
This Demonstration illustrates Sainte-Laguë's method of allocating parliamentary seats.

[more]

The party with the most electoral votes obtains the first seat. Each subsequent seat is then awarded to the party for which the quantity is the largest. Here denotes the number of votes party has received in the election, while is the number of parliamentary seats already allocated to party .

In the pie chart, the inner ring shows the actual electoral votes, while the outer ring displays the number of seats awarded.

[less]

Contributed by: Helmut Knaust (June 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

This method is currently used in countries around the world. It was also used in the United States from 1842–1852 and 1901–1941 to apportion House seats to states according to their population (under the name "Webster method").

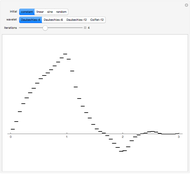
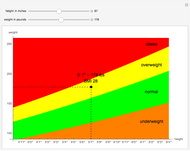
The method does not guarantee that a party with the majority of votes receives a majority in parliament (see the thumbnail illustration). This may explain why some countries replace 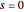(no seat allocated so far) by 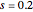, thus giving a slight preference to larger parties over marginal parties.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send