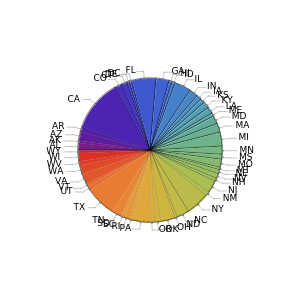
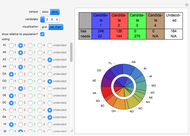
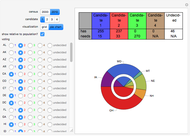
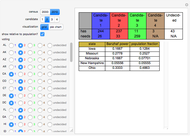
The Banzhaf Power Index of States for Presidential Candidates

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
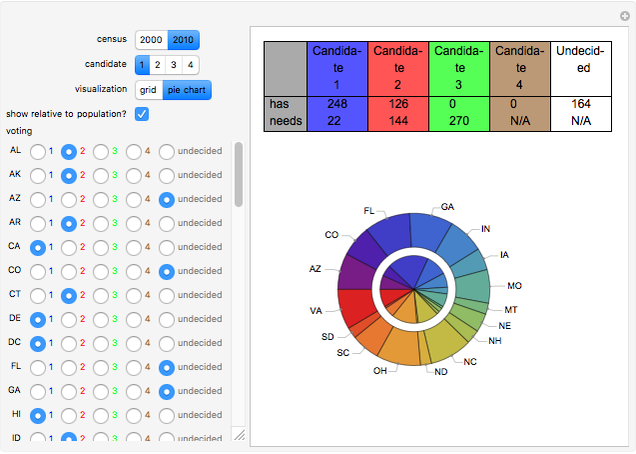
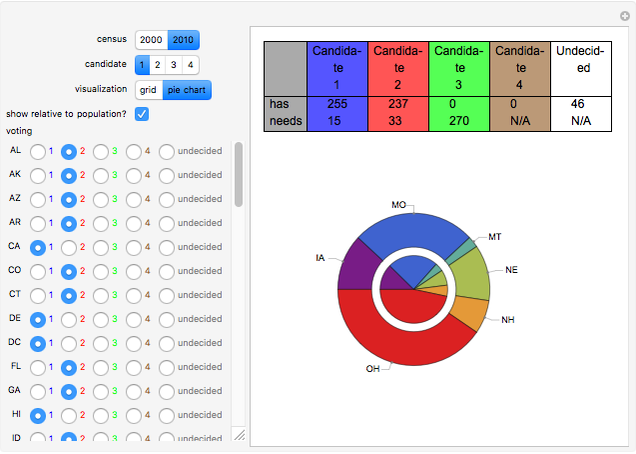
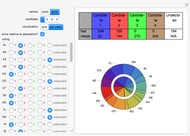
Pursuant to article II section 1 of the United States Constitution and the 12th amendment, the United States elects a president by first having each state cast a specified number of votes in an electoral college. By tradition, almost all states cast their vote as a block, all for the candidate receiving the most votes from voters within the state (the popular vote). To elect a president via the electoral college requires at least a 270 vote majority of the 538 total votes. Absent attaining such a majority, each state votes (through its membership in the House of Representatives) from among the top three candidates in the electoral college, and it takes 26 states to win via this method.
[more]
Contributed by: Seth J. Chandler (April 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
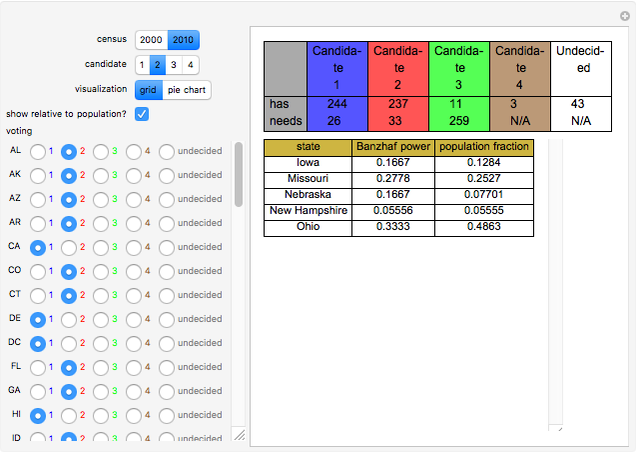
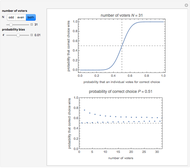
The method for computing the Banzhaf power index, along with a Mathematica program, is found in J. M. Bilbao, J. R. Fernández, A. J. Losada, and J. J. López, "Generating Functions for Computing Power Indices Efficiently," TOP, 8, 2000, pp. 191–213. (TOP is published by Springer and is an official journal of the Spanish Society of Statistics and Operations Research.)
Currently two states (Maine and Nebraska) do not necessarily vote as a block in the electoral college. This Demonstration ignores that complication and assumes that all states vote as a block. The computations conducted by this Demonstration would not be valid if many states failed to vote as a block in the electoral college.
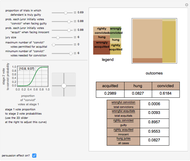
Usually, when the number of undecided states is large, the Banzhaf power index closely matches the relative populations of the remaining states, although the less populous states have a bit of an advantage owing to the automatic assignment of two votes to all states. When the number of undecided states is small, however, the Banzahf power index may depart from the relative population in ways that are difficult to predict.