Performance of a Batch Reactive Distillation System versus a Plug Flow Reactor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
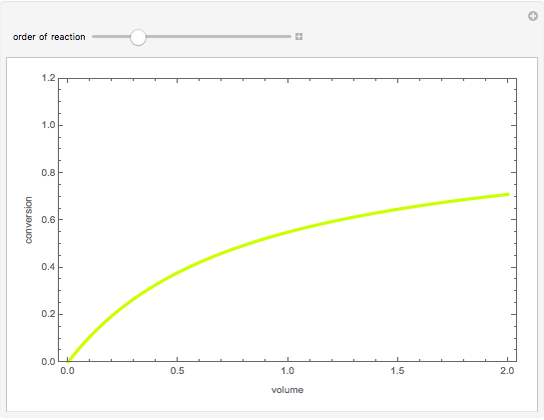
Consider the reaction sequence: 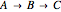 , where
, where 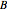 is the lightest component and
is the lightest component and 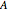 is the heaviest component. We assume that the desired product is component
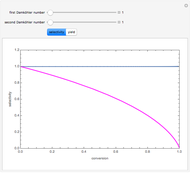
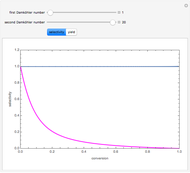
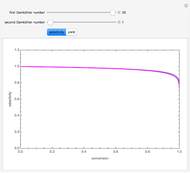
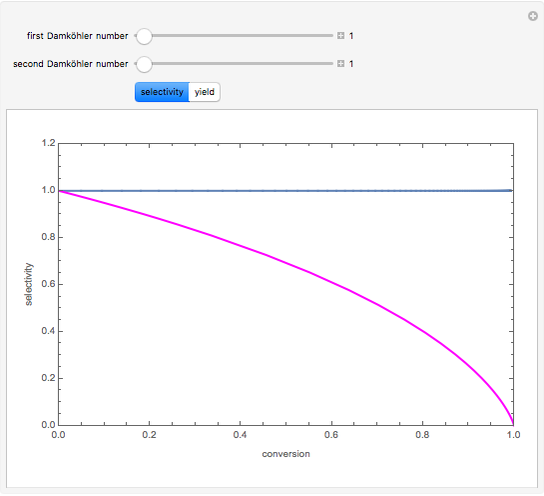
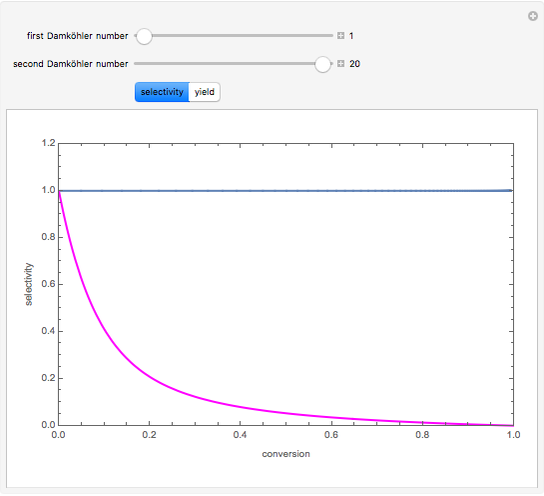
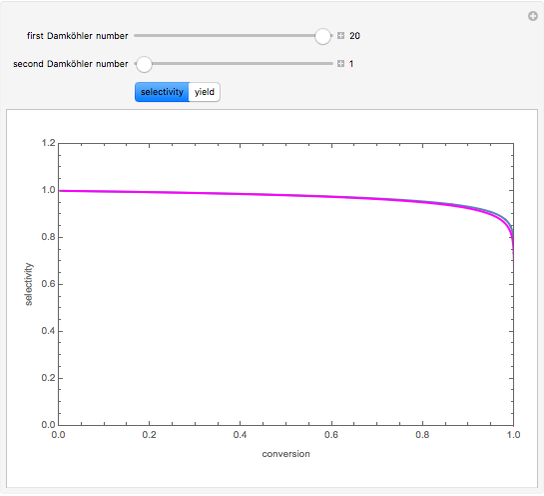
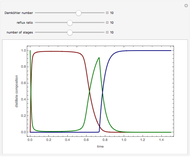
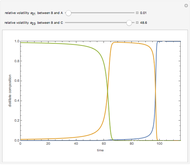
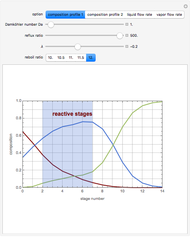
is the heaviest component. We assume that the desired product is component 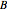 . This Demonstration compares the performances (yield and selectivity) of a plug-flow reactor (PFR) and a batch reactive distillation (BRD) system. It is found that the BRD system is superior to the PFR as far as yield and selectivity are concerned. This makes using BRD systems very attractive for such a reaction scheme and component volatilities. In order to make the calculations, the distillate rate policy is specified so that the distillate rate is proportional to the still's molar hold-up. In addition, we suppose that the reaction is taking place only in the still and that the distillate mole fraction of component
. This Demonstration compares the performances (yield and selectivity) of a plug-flow reactor (PFR) and a batch reactive distillation (BRD) system. It is found that the BRD system is superior to the PFR as far as yield and selectivity are concerned. This makes using BRD systems very attractive for such a reaction scheme and component volatilities. In order to make the calculations, the distillate rate policy is specified so that the distillate rate is proportional to the still's molar hold-up. In addition, we suppose that the reaction is taking place only in the still and that the distillate mole fraction of component 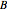 is 100%. The method of Doherty and coworkers is slightly modified by taking a small time step (0.01) and choosing the constraint
is 100%. The method of Doherty and coworkers is slightly modified by taking a small time step (0.01) and choosing the constraint 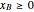 instead of equation (11) in their paper (see the Details section).
instead of equation (11) in their paper (see the Details section).
Contributed by: Housam Binous (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The first and second Damköhler numbers are defined as the dimensionless ratios of the characteristic liquid residence time to the characteristic reaction time. For example, the first Damköhler number for the BRD system is given by  , where
, where 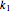 is the rate constant of the first reaction, and
is the rate constant of the first reaction, and  and
and 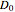 are the initial molar holdup in the reactor (the still) and the initial distillate rate, respectively.
are the initial molar holdup in the reactor (the still) and the initial distillate rate, respectively.
S. B. Gadewar, M. F. Malone and M. F. Doherty, "Selectivity Targets for Batch Reactive Distillation," Ind. Eng. Chem. Res., 39(6), 2000 pp. 1565-1575.
Permanent Citation