Pick's Theorem

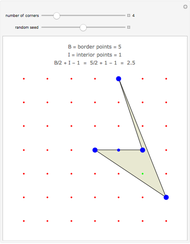
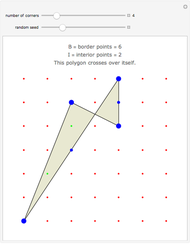
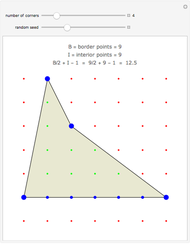
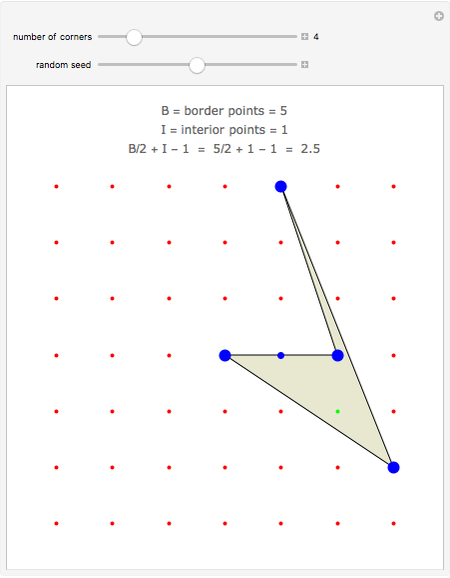
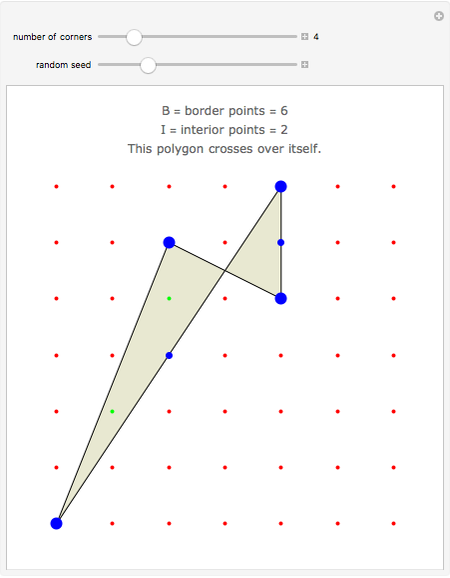
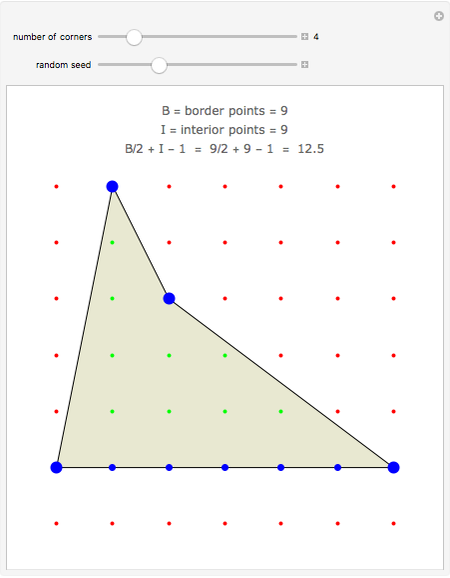
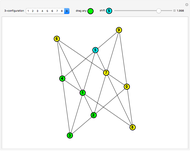
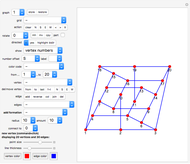
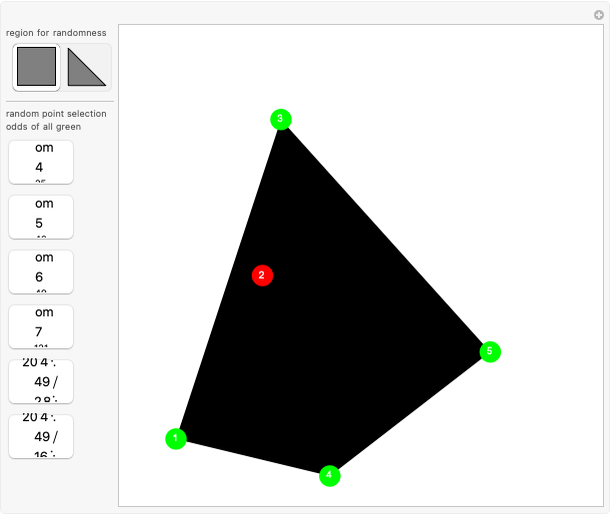
Suppose that a polygon has its corners at the points of a geoboard. (You can drag the corners.) Count the number of boundary points B and interior points I. As long as the polygon does not cross over itself, Pick's theorem gives the area as A = I + B/2 - 1. In words, the area is one less than the number of interior points plus half the number of border points.