Predator-Prey Equations Simulating an Immune Response

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
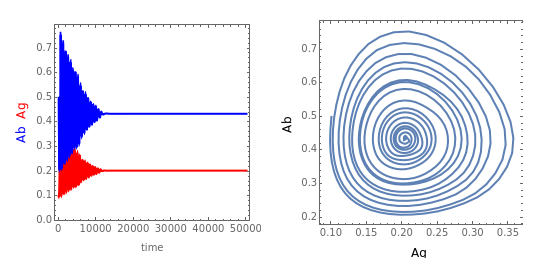
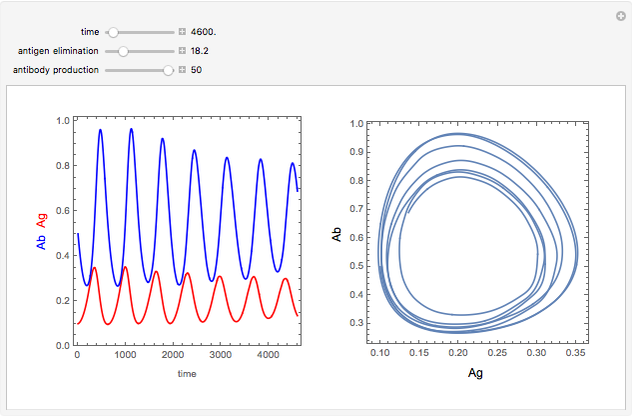
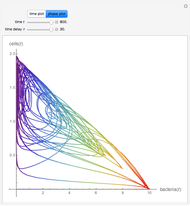
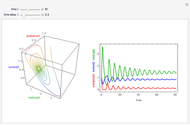
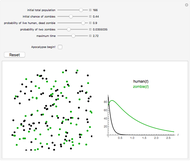
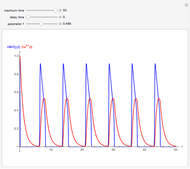
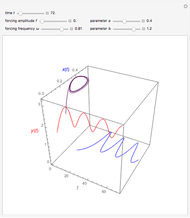
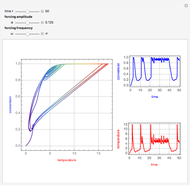
The immune response to a replicating antigen may be viewed as a problem of interacting populations of antigens and antibodies. This Demonstration analyzes a simple mathematical model of the immune response: antigen plays the role of prey and antibody the role of predator.
Contributed by: Clay Gruesbeck (January 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The model is governed by two differential equations [1]:
 ,
,
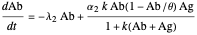 ,
,
where 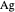 and
and  denote the concentrations of antigen and antibody,
denote the concentrations of antigen and antibody, 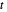 is time,
is time, 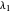 is the antigen replication rate,
is the antigen replication rate, 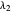 is the antibody decay rate,
is the antibody decay rate,  is an equilibrium constant,
is an equilibrium constant,  is the rate of antigen elimination,
is the rate of antigen elimination, 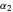 is the rate of antibody production, and
is the rate of antibody production, and  is the maximum antibody concentration the host is able to produce.
is the maximum antibody concentration the host is able to produce.
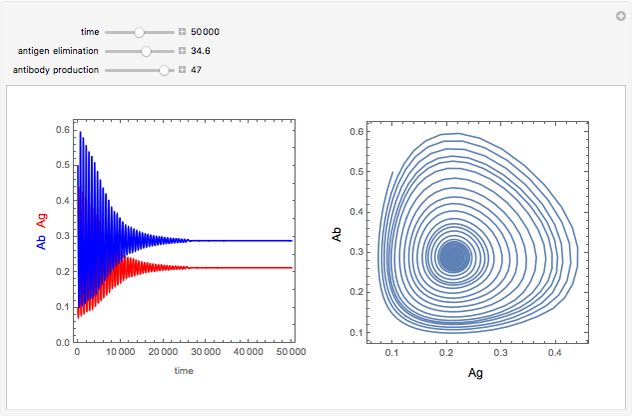
In this Demonstration, equations 1a, 1b, and 4 of [1] are solved with 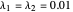 ,
,  ,
,  ,
, 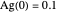 , and
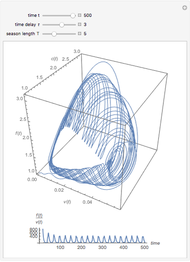
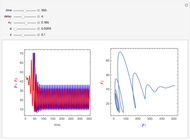
, and  ; the solution is presented in plots of antigen and antibody concentrations versus time and in a antigen-antibody phase plot.
; the solution is presented in plots of antigen and antibody concentrations versus time and in a antigen-antibody phase plot.
If  , periodic oscillations of the antigen and antibody are found; if
, periodic oscillations of the antigen and antibody are found; if 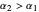 , both populations execute damped oscillations and approach a steady state, and if
, both populations execute damped oscillations and approach a steady state, and if 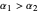 , both populations execute oscillations of increasing amplitude. During such oscillations in a real biological system, presumably either the antigen would be eliminated during an antigen minimum or the host would be eliminated during an antigen maximum.
, both populations execute oscillations of increasing amplitude. During such oscillations in a real biological system, presumably either the antigen would be eliminated during an antigen minimum or the host would be eliminated during an antigen maximum.
Reference
[1] G. I. Bell, "Predator-Prey Equations Simulating an Immune Response," Mathematical Biosciences, 16(3–4),1973 pp. 291–314. doi:10.1016/0025-5564(73)90036-9.
Permanent Citation