Kermack-McKendrick Epidemic Model with Time Delay

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
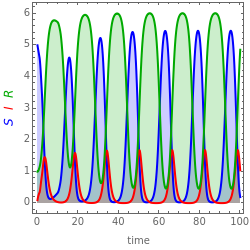
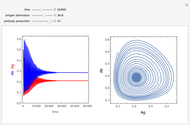
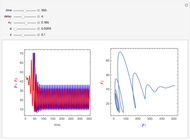
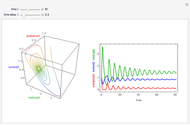
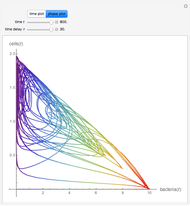
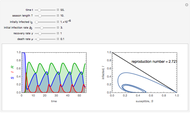
This Demonstration solves a system of three differential equations with time delays, corresponding to a Kermack–McKendrick epidemic model.
Contributed by: Clay Gruesbeck (December 2012)
Open content licensed under CC BY-NC-SA
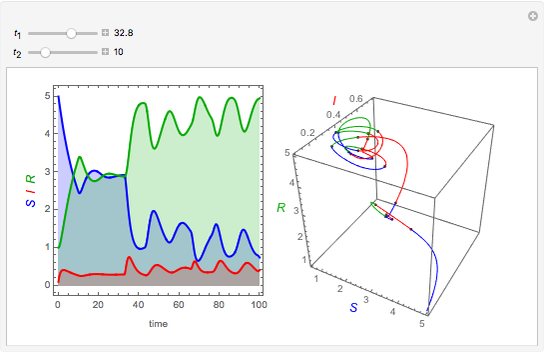
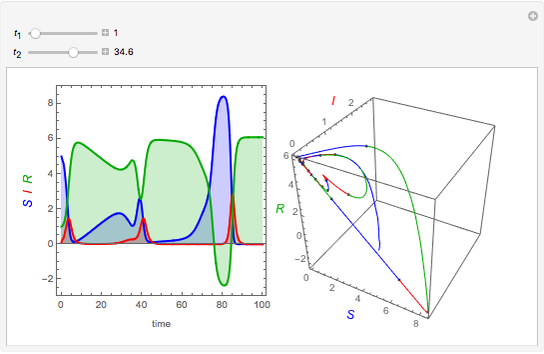
Snapshots
Details
The Kermack–McKendrick model simulates the number of people infected with a contagious illness in a closed population over time. It assumes that the population size is fixed, that the incubation period of the infectious agent is instantaneous, and that the duration of infectivity is the same as the duration of the disease. This model is modified by incorporating a delay time representing the period for incubation, which is the time during which infectious agents develop in the vector; only after that time does the infected vector itself becomes infective, and a delay time for the duration of the infectivity. The model consists of three coupled delay ordinary differential equations and three initial history functions.
 ,
,
 ,
,
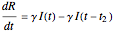 ,
,
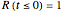 .
.
Here  is time,
is time, 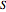 is the number of susceptible people,
is the number of susceptible people, 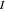 is the number of infected people,
is the number of infected people, 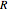 is the number of people who have recovered and developed immunity to the infection,
is the number of people who have recovered and developed immunity to the infection, 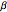 is the infection rate,
is the infection rate,  is the recovery rate,
is the recovery rate, 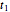 is the incubation period, and
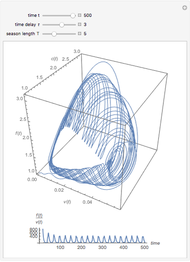
is the incubation period, and 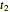 is the duration of infectivity. The infection and recovery rates are assumed to be equal to 1. The delay equations are solved using Mathematica's built-in function NDSolve and the results are shown as plots of the number of people in each group versus time and in a three-dimensional parametric plot of the three groups of people. You can change
is the duration of infectivity. The infection and recovery rates are assumed to be equal to 1. The delay equations are solved using Mathematica's built-in function NDSolve and the results are shown as plots of the number of people in each group versus time and in a three-dimensional parametric plot of the three groups of people. You can change 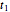 , the period of incubation, and
, the period of incubation, and 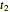 , the duration of infectivity, to follow the trajectory of the solution.
, the duration of infectivity, to follow the trajectory of the solution.
Permanent Citation