Principal Components Analysis: Application in Value at Risk and Expected Shortfall

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
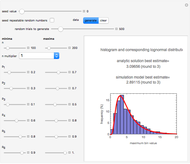
Principal Component Analysis (PCA) is used in financial risk management to reduce the dimensionality of a multivariate problem, thus creating a simpler representation of the risk factors in the dataset. Only a few judiciously chosen hypothetical variables are needed to explain a large proportion of the variability in the data. These principal components are obtained through the singular value decomposition of the return series.
[more]
Contributed by: Pichet Thiansathaporn (July 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
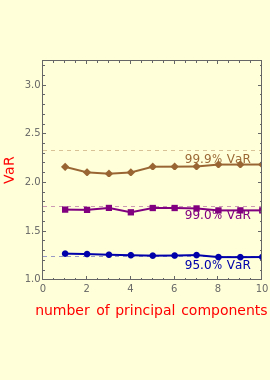
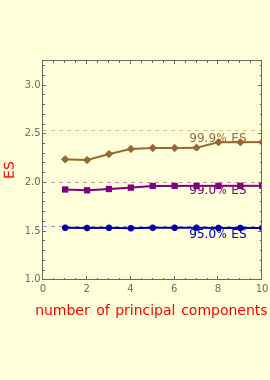
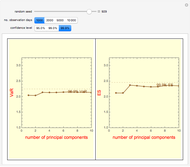
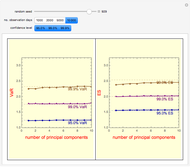
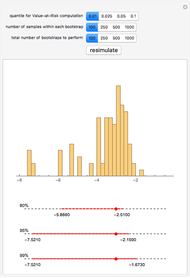
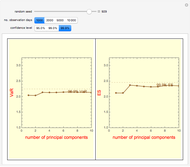
Snapshot 1: PCA VaR stabilizes when the number of principal components exceeds three
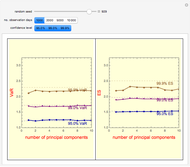
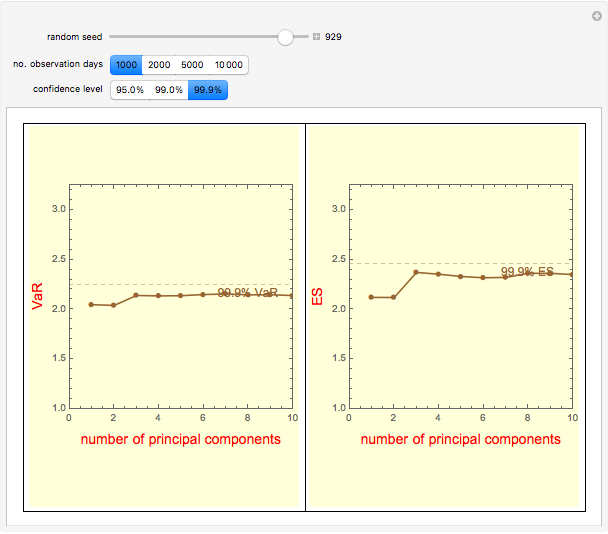
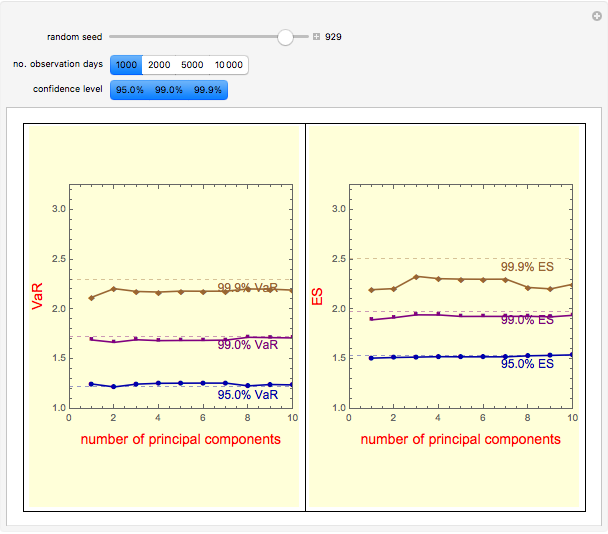
Snapshot 2: divergence of PCA VaR (plotted points) from the "true" asymptotic VaR (dashed horizontal lines) is more pronounced: (1) toward the tail of the distribution (higher confidence level); and (2) with a small number of data points (1,000 observation days)
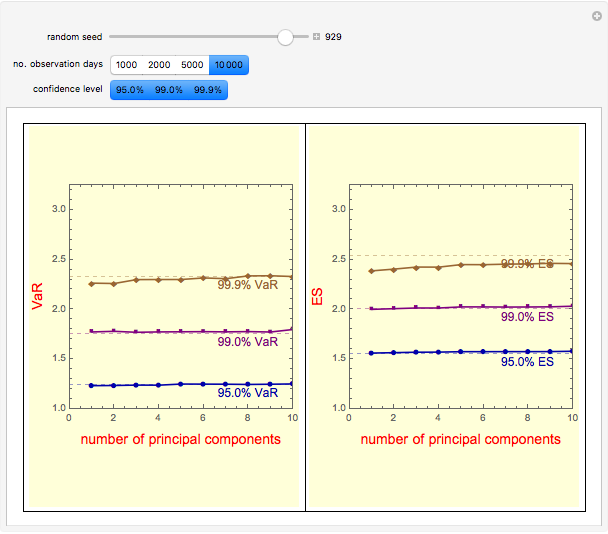
Snapshot 3: divergence decreases with a larger number of data points (10-fold increase from Snapshot 2)
Reference
[1] Kevin Dowd, Measuring Market Risk, 2nd ed., West Sussex, England: Wiley, 2005 pp. 118–125.
Permanent Citation