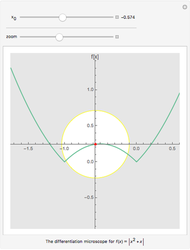
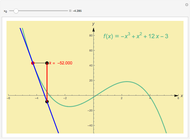
Quality of Approximation by Geometric Series

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
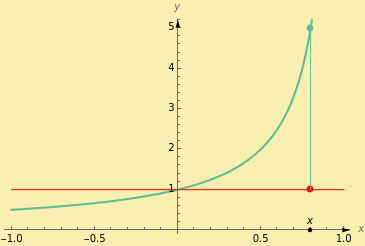
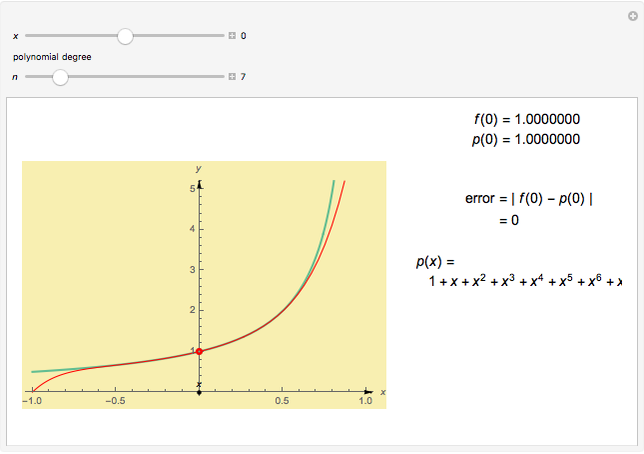
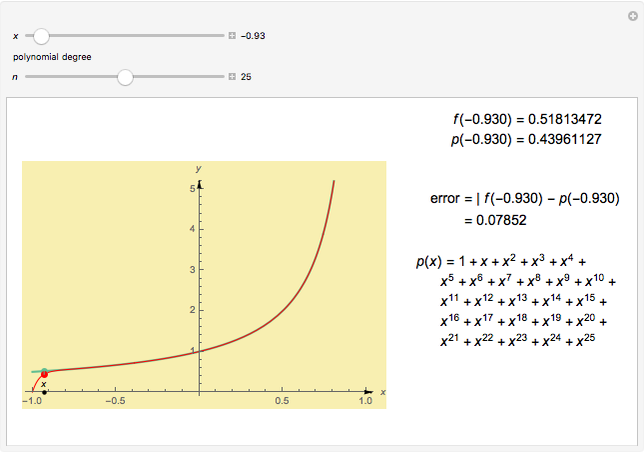
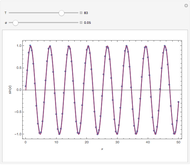
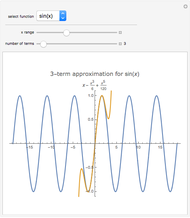
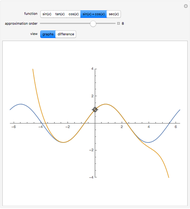
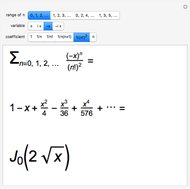
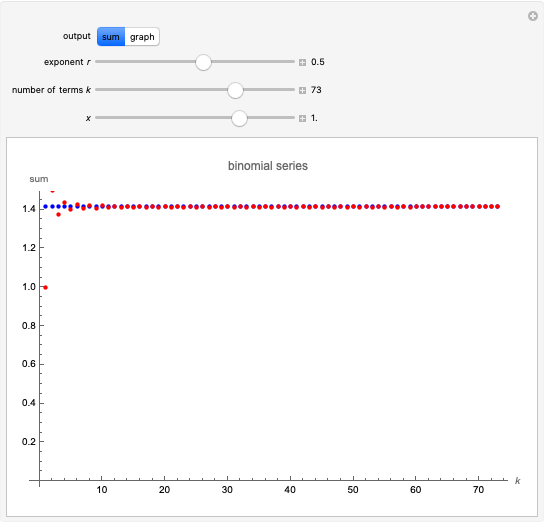
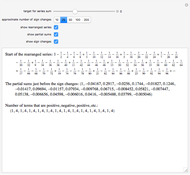
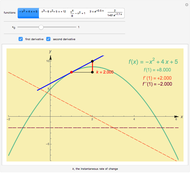
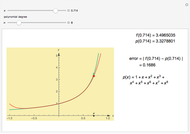
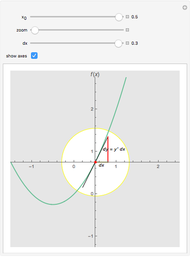
This Demonstration shows graphically and numerically the quality of approximating the function values of 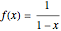 for any
for any 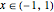 by the Taylor polynomial
by the Taylor polynomial 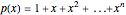 , where
, where 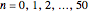 .
.
Contributed by: Reinhard Simonovits (September 2012)
With additional contributions by: Bernd Thaller
Open content licensed under CC BY-NC-SA
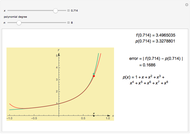
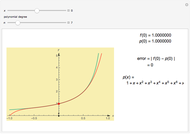
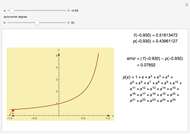
Snapshots
Details
Review questions:
Let 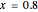 and
and  . How large is the error?
. How large is the error?
Let 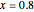 . For what
. For what  is the error less than 0.01?
is the error less than 0.01?
Let  and
and  . How large is the error?
. How large is the error?
Let  . Check the error for
. Check the error for  . (The point
. (The point  is the "best" point since it is the expansion point.)
is the "best" point since it is the expansion point.)
For  , at which
, at which  is the error largest?
is the error largest?
For  and
and 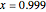 , how large is the error?
, how large is the error?
For  and
and 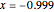 , how large is the error?
, how large is the error?
Permanent Citation