Relaxation of a Maxwell Element

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
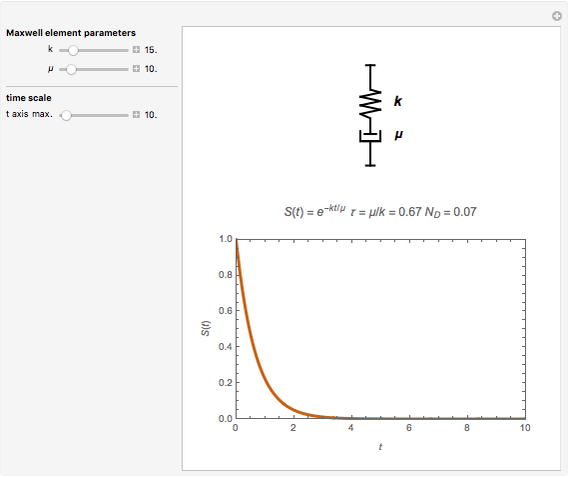
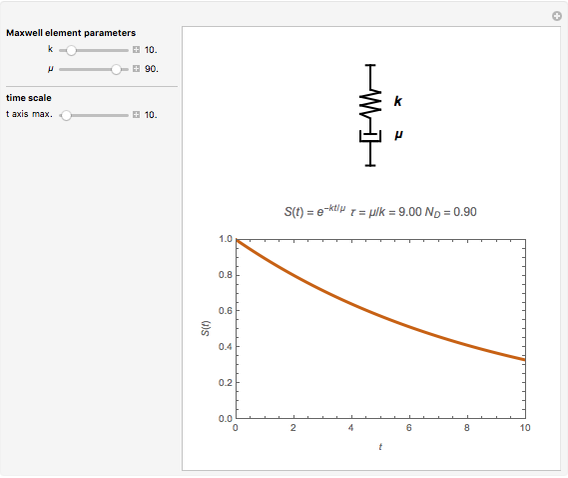
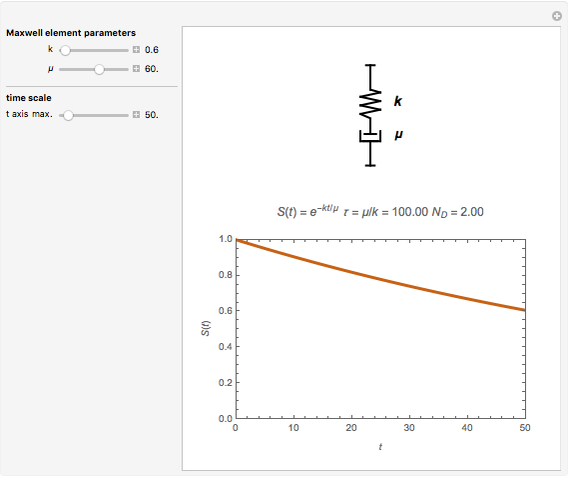
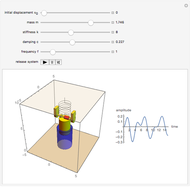
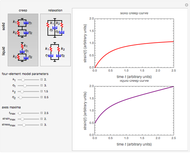
This Demonstration aids in visualization of the roles of the two components of a Maxwell element in its response to a unit step stress. It depicts the relaxation curve resulting from changes in the relative magnitudes of the elastic component's modulus (represented by a spring) and the dissipating component's viscosity (represented by a dashpot). It also displays the element's relaxation time  and the ratio between
and the ratio between  and the characteristic observation time (represented by the plot's time scale) referred to here as the Deborah number
and the characteristic observation time (represented by the plot's time scale) referred to here as the Deborah number  .
.
Contributed by: Mark D. Normand and Micha Peleg (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
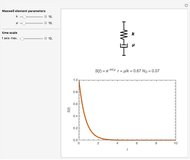
Snapshot 1: a relaxation curve with a short relaxation time  and small Deborah number
and small Deborah number 
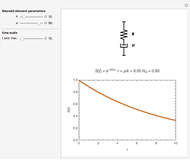
Snapshot 2: a relaxation curve with a longer relaxation time  and larger Deborah number
and larger Deborah number 
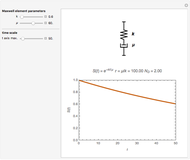
Snapshot 3: a relaxation curve with a still longer relaxation time  and even larger Deborah number
and even larger Deborah number 
Snapshot 4: apparent elastic response of an element with a very long relaxation time 
Snapshot 5: apparent viscous response of an element with a very short relaxation time 
This Demonstration calculates and plots the stress relaxation curve of a Maxwell element subjected to a unit step stress described by the equation 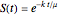 where
where  is the dissipating stress at time
is the dissipating stress at time  ,
,  is the elastic component's modulus and
is the elastic component's modulus and  the viscosity. The element's relaxation time,
the viscosity. The element's relaxation time,  , is the ratio
, is the ratio  , here with arbitrary time units. The Deborah number,
, here with arbitrary time units. The Deborah number,  , is represented here by the ratio
, is represented here by the ratio 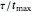 , where
, where  is the maximum value of the plot's time axis. The values of the parameters
is the maximum value of the plot's time axis. The values of the parameters  ,
,  , and
, and  are entered with sliders. An ideogram of the Maxwell element (a spring-dashpot in series combination) is displayed above the plot. Also shown are the stress relaxation equation and the current calculated numeric values of
are entered with sliders. An ideogram of the Maxwell element (a spring-dashpot in series combination) is displayed above the plot. Also shown are the stress relaxation equation and the current calculated numeric values of  and
and  .
.
Permanent Citation