Details

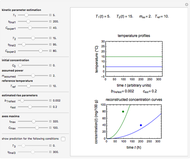
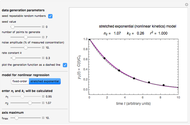
Snapshot 1: the reconstructed TVBN formation curves of the two endpoints shown in the thumbnail

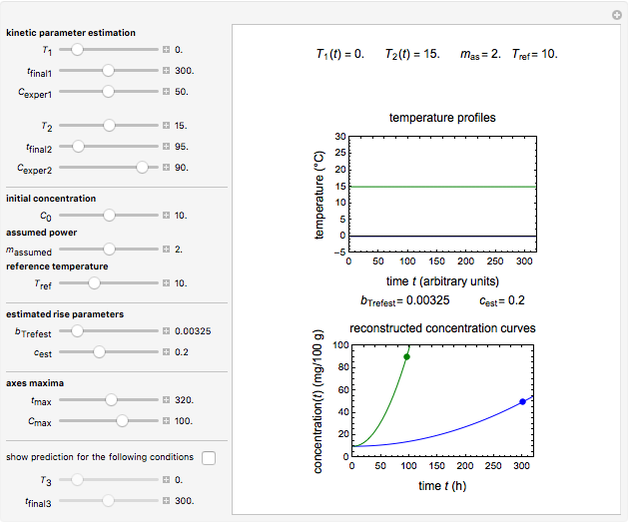
Snapshot 2: a predicted TVBN formation curve at a third temperature calculated from the two endpoints shown in snapshot 1

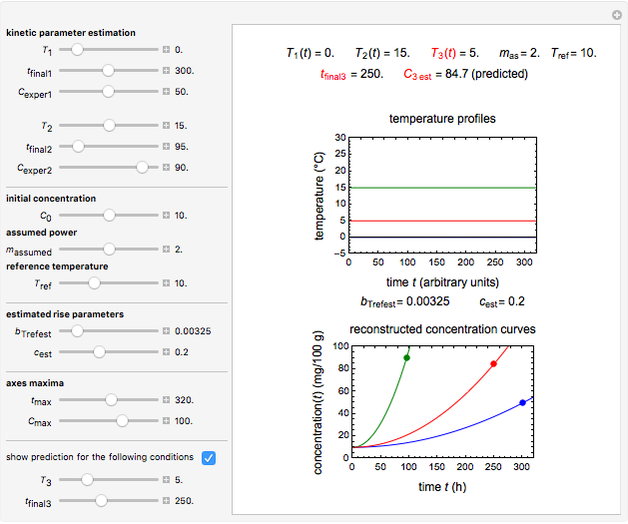
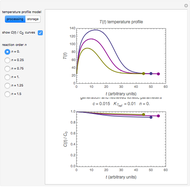
Snapshot 3: two entered hypothetical TMA experimental endpoints at two temperatures

Snapshot 4: the reconstructed TMA formation curves of the two endpoints shown in snapshot 3

Snapshot 5: a predicted TMA formation curve at a third temperature calculated from the two endpoints shown in snapshot 4

Microbial spoilage of fresh fish at ambient temperatures or in refrigerated storage produces a characteristic repulsive off-odor. Chemical determination of the concentration of volatiles such as trimethylamine (TMA) and/or of the total volatile biological nitrogen (TVBN) is faster than determining the microbial count, and hence can be used as an alternative to monitor fish freshness and determine their shelf life. Frequently, plots of the TMA and TVBN concentration vs. time during fish fillets' isothermal storage have a typical shape [1, 2]. It can be described by the empirical power-law model 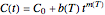, where 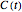is the momentary concentration, usually expressed as mg/100g; 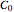the initial concentration in the same units, which can be zero; a temperature-dependent "rate parameter" that is characteristic to the fish species and influenced by any pre-treatment it might have received, e.g. added antibiotic or partial dehydration; is the time in hours or days; and 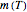is a dimensionless "shape characteristic parameter", usually a weak function of temperature that can be assumed constant, 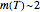, as first approximation.

It is assumed that the temperature dependence of the rate parameter follows the exponential model , a simpler substitute for the traditional Arrhenius equation [3–5], where is the rate parameter’s value at an arbitrary reference temperature in the pertinent range, and a constant having temperature reciprocal units. All temperatures are in °C.

The traditional database to extract kinetic parameters has been a set of experimentally determined concentration versus time curves at different constant temperatures, which requires considerable effort and time. It has been shown that much of this effort can be saved by determining only the endpoints of such curves and using them to calculate the kinetic parameters by numerically solving triplets or pairs of algebraic or differential equations [3–5]. The method, however, has only been applied to microbial survival and chemical degradation—that is, to decay processes where the measured quantity continuously declines. In this Demonstration we apply the endpoints method to fish spoilage kinetics when monitored by following the rise of the TMA or TVBN concentration. With the above model and a fixed shape parameter 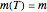, this translates to the pair of simultaneous equations 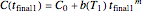and 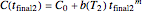, where is defined by the exponential model and and are the two unknowns. In this Demonstration the two equations are solved graphically, rather than guessing the parameter values.

To start the and calculations, enter the two experimentally determined or contemplated TMA or TVBN concentrations and corresponding temperatures and times with sliders. Similarly entered are the known initial concentration 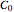, the assumed power 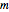, and a chosen reference temperature 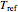, in the neighborhood of 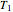and .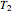

To estimate the unknown kinetic parameters and , move their sliders until the two reconstructed curves generated with the model pass through the two endpoints. The sliders’ positions when the curves and endpoints match mark these parameters’ values, which are also displayed above the bottom plot for clarity.

Once obtained in this way, these kinetic parameters can be used to predict the two volatiles’ formation curve at a chosen third temperature by checking the "show prediction for the following conditions" box and setting the positions of the corresponding temperature 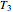and time 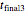sliders’ positions. The predicted curve and TMA or TVBN concentration are displayed in red.

Note that not all entered endpoints that the program allows have corresponding and values.

References

[1] K. Koutsoumanis and G.-J. E. Nychas, "Application of a Systematic Experimental Procedure to Develop a Microbial Model for Rapid Fish Shelf Life Predictions," International Journal of Food Microbiology, 60(2–3), 2000 pp. 171−184.

[2] T. N. Tsironi and P. S. Taoukis, "Modeling Microbial Spoilage and Quality of Gilthead Seabream Fillets: Combined Effect of Osmotic Pretreatment, Modified Atmosphere Packaging, and Nisin on Shelf Life," Journal of Food Science, 75(4), 2010 pp. M243–M251.

[3] M. Peleg, M. D. Normand, and A. D. Kim, "Estimating Thermal Degradation Kinetics Parameters from the Endpoints of Non-isothermal Heat Processes or Storage," Food Research International, 66, 2014 pp. 313–324.

[4] M. Peleg, A. D. Kim, and M. D. Normand, "Predicting Anthocyanins' Isothermal and Non-isothermal Degradation with the Endpoints Method," Food Chemistry, 187, 2015 pp. 537–544.

[5] M. Peleg, M. D. Normand, and T. R Goulette, "Calculating the Degradation Kinetic Parameters of Thiamine by the Isothermal Version of the Endpoints Method," Food Research International, 79, 2016 pp. 73–80.