Extending the Square Root Growth Rate Model to Lethal Low Temperatures

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
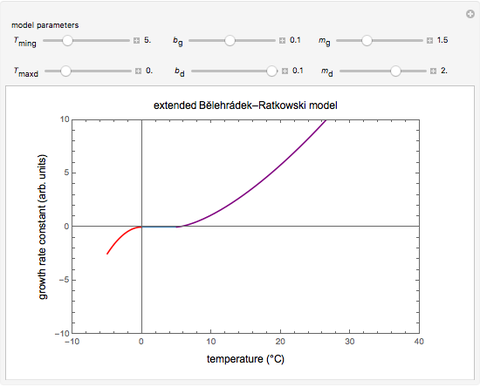
When the temperature of a microbial population is lowered beyond a certain level, its growth ceases and can become inactive. The phenomenon is reversed upon heating. The temperature effect on the growth rate above the minimal temperature needed for growth has been frequently described by Ratkowski's square root model, a simple, useful variant of the Bĕlehrádek model. This Demonstration provides graphical visualization of an extended version of these models in the region where growth ceases and turns into inactivation or vice versa. The extended model has been constructed by mirroring the temperature effect in the two regimes and allowing for an intermediate temperature range where the population size remains practically unchanged.
Contributed by: Mark D. Normand and Micha Peleg (May 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
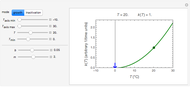
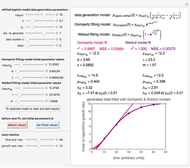
Snapshot 1: the growth rate's temperature dependence of a hypothetical bacterium according to the traditional square root model
Snapshot 2: the cold inactivation rate's temperature dependence of a hypothetical bacterium according to the extended model
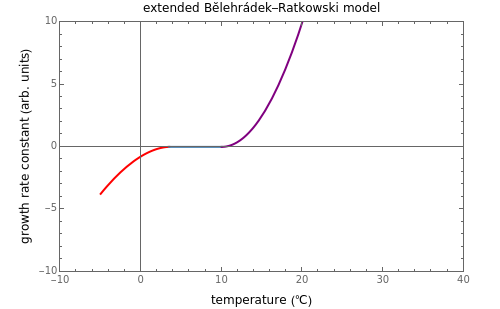
Snapshot 3: the temperature effect on the growth and inactivation rates of a hypothetical thermophilic bacterium
Snapshot 4: the temperature effect on the growth and inactivation rates of a hypothetical mesophilic bacterium
Snapshot 5: the temperature effect on the growth and inactivation of a hypothetical psychrophilic bacterium
Ratkowski’s square root model was originally written in the form
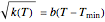 ,
,
where 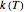 is the growth rate parameter, usually the sigmoid isothermal growth curve’s slope at its inflection point,
is the growth rate parameter, usually the sigmoid isothermal growth curve’s slope at its inflection point, 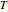 the temperature and
the temperature and  the temperature below which growth ceases [1, 2]. The model can also be written in the general form:
the temperature below which growth ceases [1, 2]. The model can also be written in the general form:
If 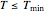 ,
,
0.,
else 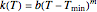 ,
,
where 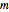 can, but need not always, be equal to 2 [2–4]. Notice that without the added "If" statement, the original model's equation implies that at
can, but need not always, be equal to 2 [2–4]. Notice that without the added "If" statement, the original model's equation implies that at 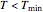 the rate constant rises if
the rate constant rises if 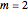 , or becomes a complex number if
, or becomes a complex number if 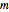 is a noninteger.
is a noninteger.
In reality, it can be expected that at temperatures below  , growth not only ceases but turns into mortality, causing the population size to decrease. In terms of the model, at
, growth not only ceases but turns into mortality, causing the population size to decrease. In terms of the model, at 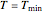 , the growth rate
, the growth rate  changes sign and becomes negative, signifying inactivation.
changes sign and becomes negative, signifying inactivation.
For a qualitative account of such scenarios, we assume that the growth and inactivation regimes can be separated by a stationary region where for all practical purposes 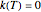 , and that at least initially, the
, and that at least initially, the 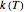 versus
versus 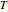 curve in the inactivation regime mirrors that in the growth regime, albeit with different parameters having different magnitudes. If these assumptions hold, a
curve in the inactivation regime mirrors that in the growth regime, albeit with different parameters having different magnitudes. If these assumptions hold, a  versus
versus 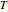 curve that describes all three regimes will have the form:
curve that describes all three regimes will have the form:
If 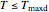 ,
,
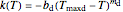 ,
,
else if  ,
,
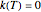 ,
,
else 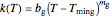 ,
,
where 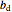 and
and 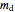 ,
, 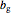 and
and  are the pairs of the decay and growth parameters, respectively, and
are the pairs of the decay and growth parameters, respectively, and 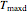 and
and 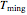 mark the region where the population size remains practically unchanged.
mark the region where the population size remains practically unchanged.
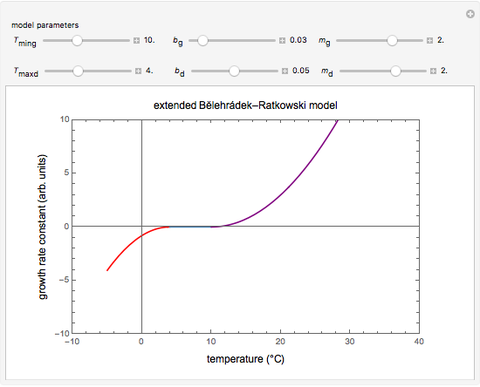
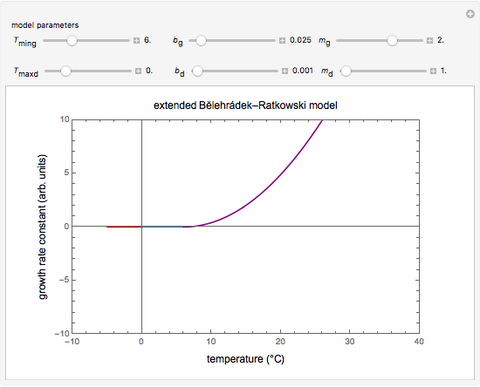
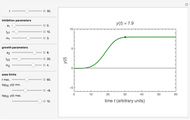
This Demonstration provides graphical visualization of the expanded version of the Bĕlehrádek–Ratkowski model in the transition region from growth to inactivation or vice versa with sliders to set the model parameters 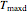 ,
, 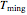 ,
, 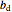 ,
, 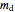 ,
, 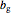 and
and  .
.
Notice that in Ratkowski's original model  is a special case of the expanded model where
is a special case of the expanded model where  ,
, 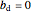 and
and 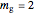 . Where
. Where  ,
, 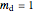 and
and  , the model renders an inverted image of
, the model renders an inverted image of  reminiscent of the shape of a curve following the log-logistic inactivation model.
reminiscent of the shape of a curve following the log-logistic inactivation model.
The purpose of this Demonstration is only to illustrate the extended version of the Bĕlehrádek–Ratkowski model, not to match the behavior of any particular micro- or macroorganism [3]. Therefore, not all the parameter combinations allowed by the controls necessarily represent real-life growth/inactivation or inactivation/growth scenarios. Also, this Demonstration addresses only the growth/inactivation rate constant, ignoring the other kinetic parameters that account for the shape of the entire inactivation/growth curve [5].
References
[1] D. A. Ratkowski, J. Olley, T. A. McMeekin and A. Ball, "Relationship between Temperature and Growth Rate of Bacterial Cultures," Journal of Bacteriology, 149(1), 1982 pp. 1–5. jb.asm.org/content/149/1/1.full.pdf+html.
[2] T. Ross, "Bĕlehrádek-Type Models," Journal of Industrial Microbiology and Biotechnology, 12(3–5), 1993 pp. 180–189. doi:10.1007/BF01584188.
[3] J.-F. Briere, P. Pracros, A.-Y. Le Roux and J.-S. Pierre, "A Novel Rate Model of Temperature-Dependent Development for Arthropods," Environmental Entomology, 28(1), 1999 pp. 22–29. doi:10.1093/ee/28.1.22.
[4] L. Huang, C.-A. Hwang and J. Phillips, "Evaluating the Effect of Temperature on Microbial Growth Rate—The Ratkowski and a Bĕlehrádek-Type Models," Journal of Food Science, 76(8), 2011 pp. M547–M557. doi:10.1111/j.1750-3841.2011.02345.x.
[5] M. Peleg and M. G. Corradini, "Microbial Growth Curves: What the Models Tell Us and What They Cannot," Critical Reviews in Food Science and Nutrition, 51(10), 2011 pp. 917–945. doi:10.1080/10408398.2011.570463.
Permanent Citation