Reversal-Addition Related Systems

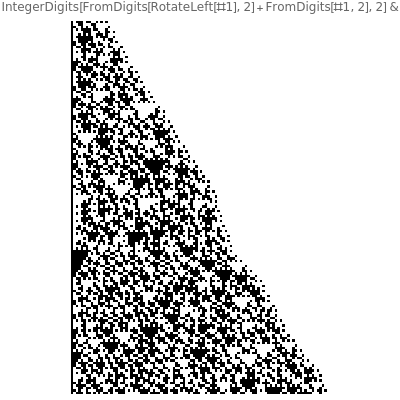
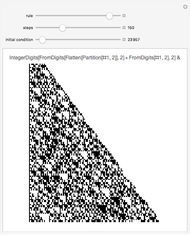
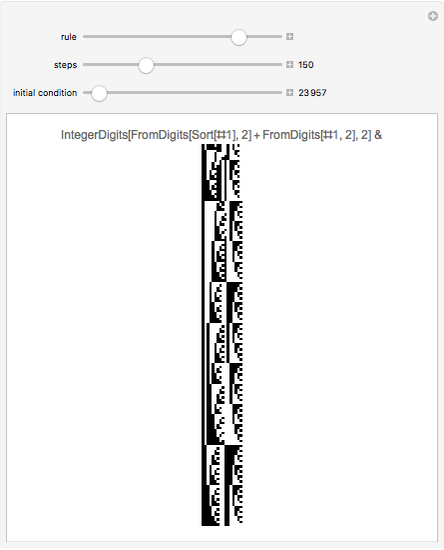
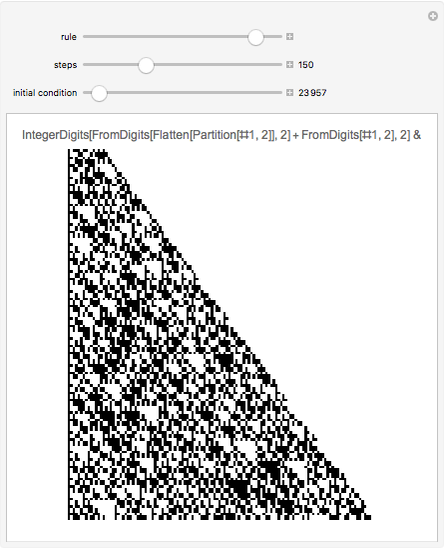
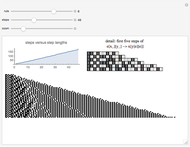
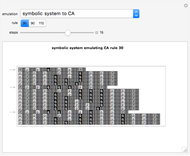
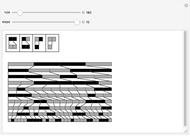
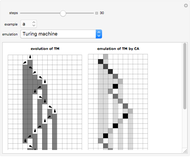
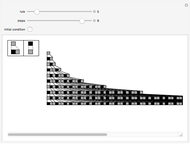
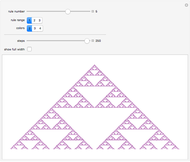
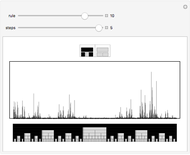
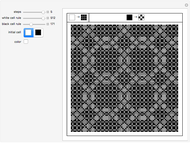
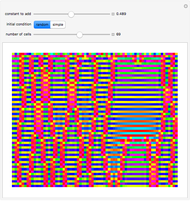
Take a number in binary, reverse its digits, and then add it to the original number. Iterating this process produces interesting behavior. This particular system is called "reversal-addition" and was considered by Stephen Wolfram in A New Kind of Science.

This Demonstration looks at generalizations of this system, where additional Mathematica list primitives (Accumulate, Append, Differences, Flatten, ListConvolve, ListCorrelate, Most, Partition, Rest, RotateLeft, RotateRight, and Sort) are used instead of Reverse. Even with these basic operations on lists of 0's and 1's, we immediately recognize complex behavior, demonstrating that small sets of Mathematica primitives are enough to produce such behavior.