Schrödinger Wavefunctions in a Continuously Varying Potential
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
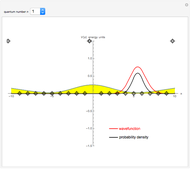
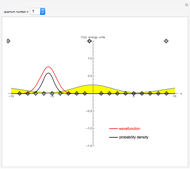
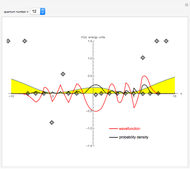
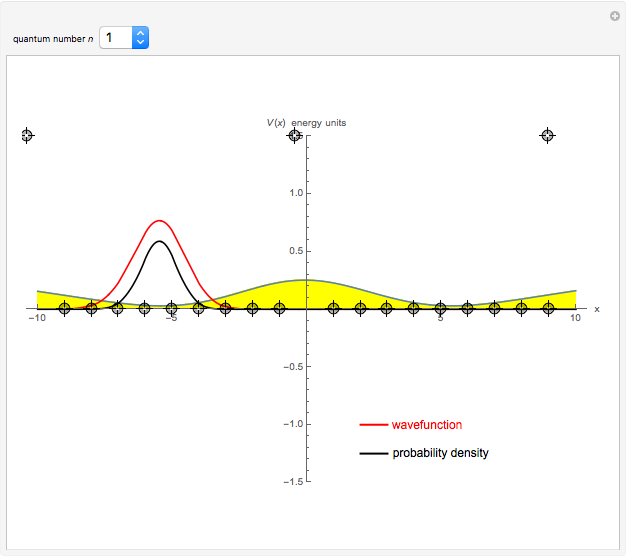
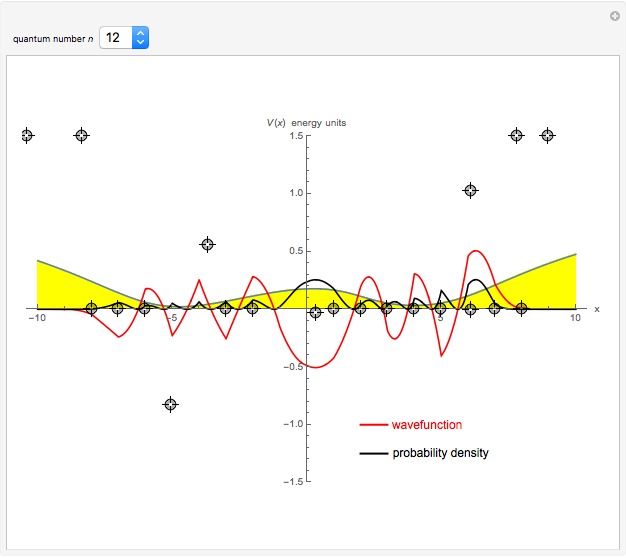
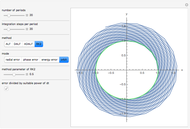
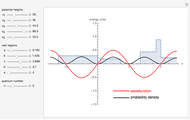
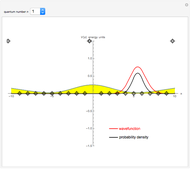
This Demonstration shows solutions of the one-dimensional Schrödinger equation in a potential-energy field 
, which can be varied by moving a series of locators. A quantum number 
(from 1 to 20) can be selected. The Schrödinger equation is then solved numerically for the wavefunctions 
, which are plotted in red, in arbitrary units. The black curves show the corresponding probability densities 
. The potential energy 
is scaled in units of 
.
Contributed by: Srivishnupreeth Rendla (July 2016)
With additional contributions by: Robert Morris
(Wolfram Summer Camp 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The snapshots show that a small change in the potential can result in a very large variation of the wavefunction.
References
[1] A. Messiah, Quantum Mechanics, New York: John Wiley & Sons, 1958.
[2] R. Shankar, Principles of Quantum Mechanics, 2nd ed., New York: Plenum, 1994.
Nonlinear Wave Equations
Stephen Wolfram and Rob Knapp
Eigenstates of the Quantum Harmonic Oscillator Using Spectral Methods
Housam Binous
Peregrine Soliton with Controllable Center in the Causal Interpretation of Quantum Mechanics
Klaus von Bloh
Acceleration of Particles in a Wave Obeying the Korteweg-de Vries Equation
Klaus von Bloh
On the Stability Limit of Leapfrog Methods
Ulrich Mutze
Trajectories of a Solitary Wave for the KdV Equation with Variable Coefficients
Klaus von Bloh
Soliton Trajectories for the Kadomtsev-Petviashvili Equation
Klaus von Bloh
Time Evolution of Quantum-Mechanical Harmonic Oscillator with Time-Dependent Frequency
Michael Trott with permission of Springer.
Linear Multistep Methods for First-Order ODEs
Wusu Ashiribo Senapon and Akanbi Moses Adebowale
Testing Second-Order Integrators for Motion of a Charge in a Homogeneous Magnetic Field
Ulrich Mutze
