Exact Solution for Rectangular Double-Well Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
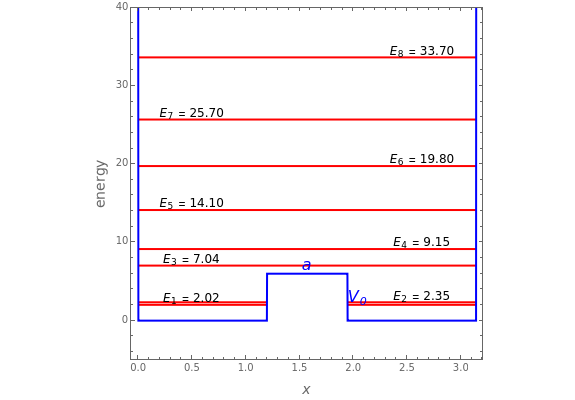
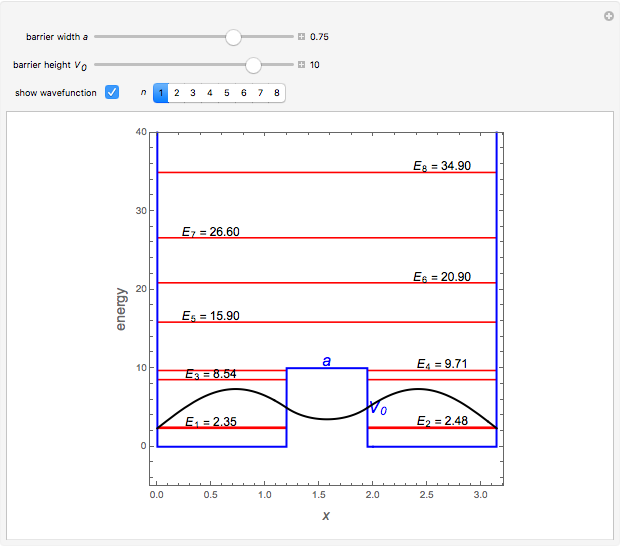
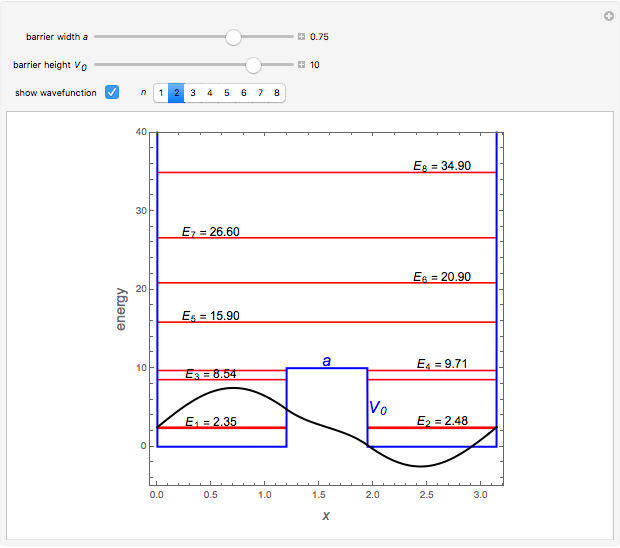
It is possible to derive exact solutions of the Schrödinger equation for an infinite square well containing a finite rectangular barrier, thus creating a double-well potential. The problem was previously approached using perturbation theory [1]. We consider the potential 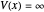 for
for 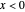 and
and 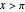 ,
, 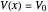 for
for 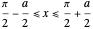 , and
, and  elsewhere. We set
elsewhere. We set 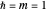 for convenience. Solutions of the Schrödinger equation
for convenience. Solutions of the Schrödinger equation 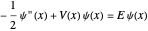 have the form of particle-in-a-box eigenfunctions in three connected segments. For the unperturbed problem, the normalized eigenstates are
have the form of particle-in-a-box eigenfunctions in three connected segments. For the unperturbed problem, the normalized eigenstates are 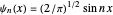 with
with  , for
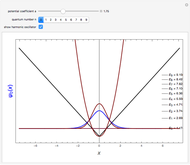
, for  . The computations for the barrier problem are spelled out in the Details section. You can display eigenvalues and eigenfunctions up to
. The computations for the barrier problem are spelled out in the Details section. You can display eigenvalues and eigenfunctions up to 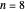 . As the barrier increases in height and width, the
. As the barrier increases in height and width, the 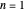 and
and 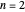 levels approach degeneracy. The linear combinations
levels approach degeneracy. The linear combinations 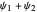 and
and 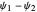 then approximate the localized states
then approximate the localized states 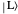 and |R⟩, respectively.
and |R⟩, respectively.
Contributed by: S. M. Blinder (May 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
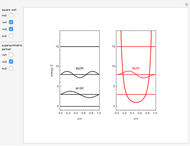
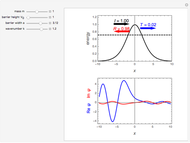
Snapshot 1: unperturbed particle-in-a-box eigenstates
Snapshots 2, 3: for larger barriers, the 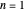 and
and 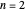 levels approach degeneracy, as do, to a lesser extent, the
levels approach degeneracy, as do, to a lesser extent, the  and
and 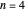 levels
levels
Even solutions, with 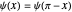 , have the form
, have the form
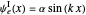 for
for  (which fulfills the boundary condition
(which fulfills the boundary condition 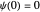 ),
),
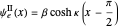 for
for 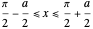 (which is even about
(which is even about  ),
),
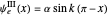 for
for  (which fulfills the boundary condition
(which fulfills the boundary condition 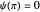 ).
).
Odd solutions, with 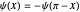 , have the form
, have the form
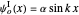 for
for 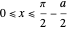 (same as the even solutions),
(same as the even solutions),
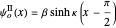 for
for  (which is odd about
(which is odd about  ),
),
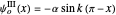 for
for 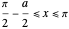 (which also fulfills the boundary condition
(which also fulfills the boundary condition  ).
In regions I and III, the energy eigenvalues follow from
).
In regions I and III, the energy eigenvalues follow from 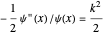 . In region II, we find
. In region II, we find 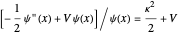 . Since these energies must be equal,
. Since these energies must be equal, 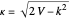 .
.
The connection formulas for the two region boundaries are most conveniently expressed in terms of the logarithmic derivatives. At 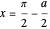 , for example,
, for example,  , and analogously for
, and analogously for  and
and 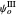 . This leads to the transcendental equations:
. This leads to the transcendental equations:
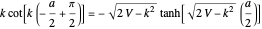 for the even eigenstates,
for the even eigenstates,  and
and
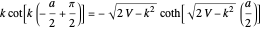 for the odd eigenstates,
for the odd eigenstates, 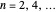 .
.
Permanent Citation