Trajectories of a Solitary Wave for the KdV Equation with Variable Coefficients

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
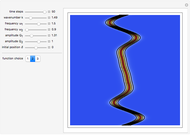
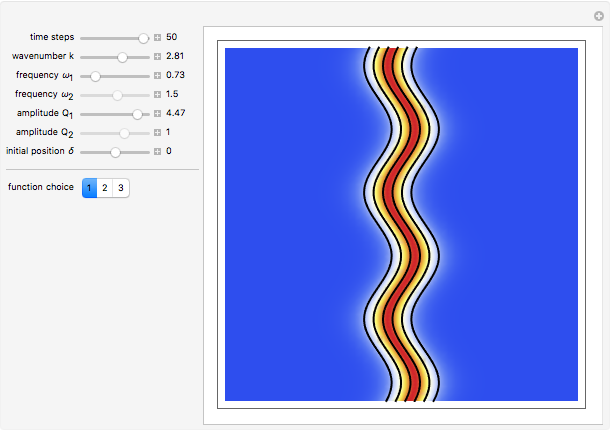
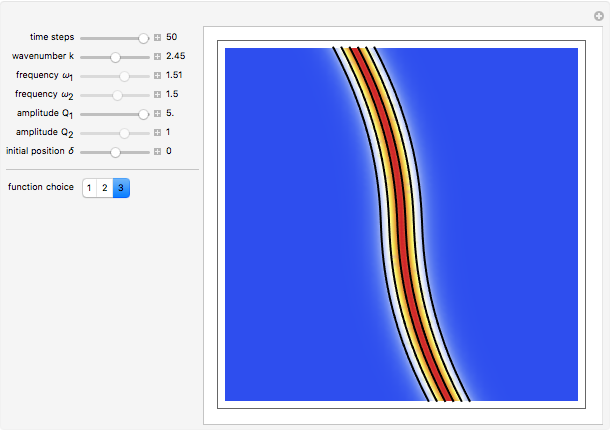
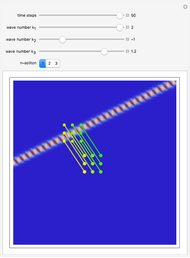
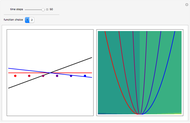
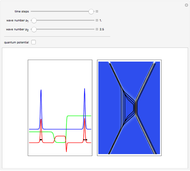
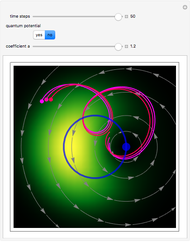
One aspect of David Bohm's causal interpretation of quantum theory is that the formalism is applicable to all linear or nonlinear partial differential equations (PDEs or nPDEs) obeying the continuity equation. In this Demonstration the trajectory concept is applied to the Korteweg–de Vries equation with variable coefficients for a singular solitary wave-like solution. The time evolution of the soliton position  could be interpreted as streamlines of the wave or as idealized test particles, which do not interact by themselves and do not influence the wave, carried by a wave that obeys the KdV equation. The system is time reversible:
could be interpreted as streamlines of the wave or as idealized test particles, which do not interact by themselves and do not influence the wave, carried by a wave that obeys the KdV equation. The system is time reversible:  . The graphics show the wave density and the trajectories in
. The graphics show the wave density and the trajectories in  space for various choices of the function
space for various choices of the function  .
.
Contributed by: Klaus von Bloh (March 2011)
Open content licensed under CC BY-NC-SA
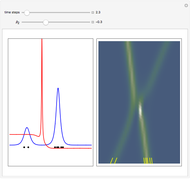
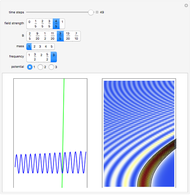
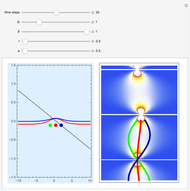
Snapshots
Details
The KdV equation, applied in a special form with variable coefficients, is:
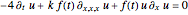 ,
,
with  and with these choices for the variable coefficient function
and with these choices for the variable coefficient function  being:
being:
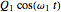 ,
,
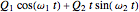 ,
,
 ,
,
and where  , and so on. The solution is a solitary wave described by:
, and so on. The solution is a solitary wave described by:
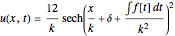 .
.
From the continuity equation 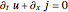 it follows
it follows  for the velocity field, which is derived from
for the velocity field, which is derived from 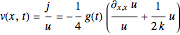 . As long as
. As long as  is integrable, there exists an analytical solution for the time evolution of a idealized particle:
is integrable, there exists an analytical solution for the time evolution of a idealized particle:
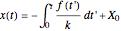 with the initial position
with the initial position  . The starting positions of the particles are linearly distributed around the peak of the wave at
. The starting positions of the particles are linearly distributed around the peak of the wave at  , where the maximum of the wave depends only on
, where the maximum of the wave depends only on  and
and  :
: 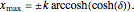 The solution of the KdV equation is based on [1].
The solution of the KdV equation is based on [1].
Reference
[1] R. Sabry, M. A. Zahran, and E. Fan, "A New Generalized Expansion Method and Its Application in Finding Explicit Exact Solutions for a Generalized Variable Coefficients KdV Equation," Physics Letters A 326, 2004 pp. 93–101.
Permanent Citation