Acceleration of Particles in a Wave Obeying the Korteweg-de Vries Equation

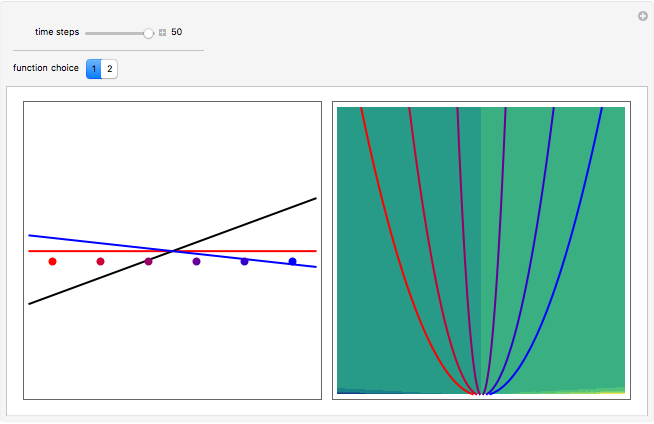
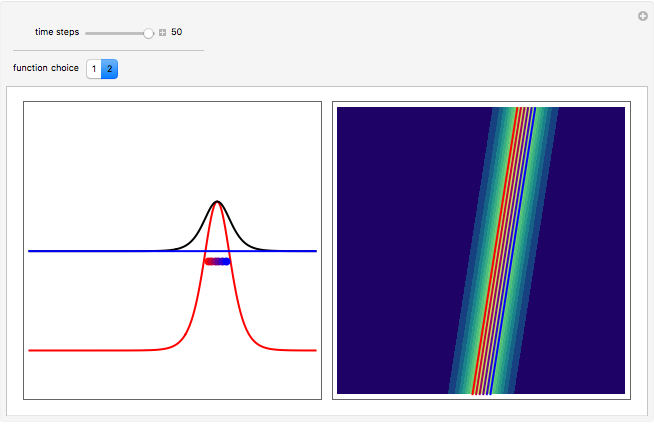
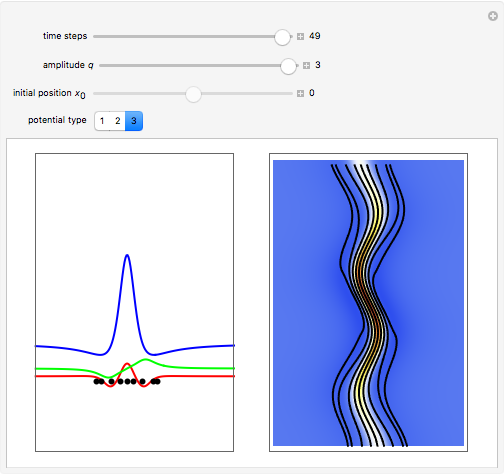
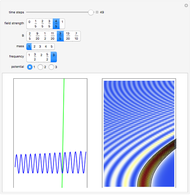
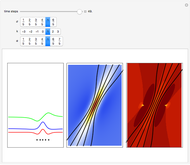
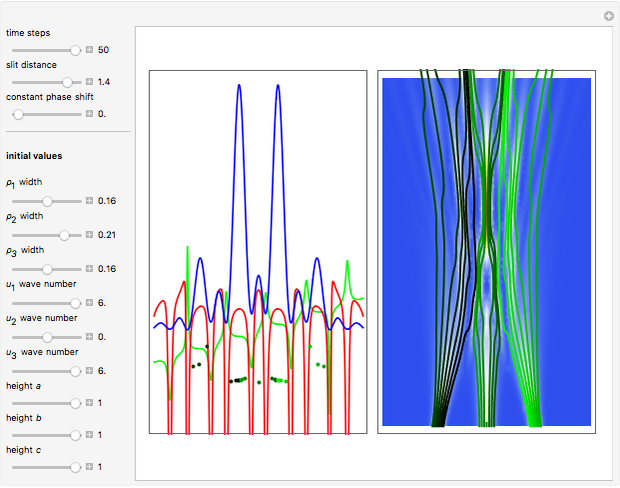
One of the advantages of the causal interpretation of quantum mechanics developed by David Bohm is that the concept of single particle trajectories in which the particles are guided by a so-called “quantum potential” can be applied to nonlinear partial differential equations obeying the continuity equation as a conservation law. 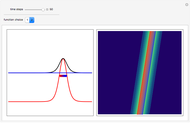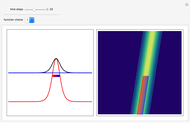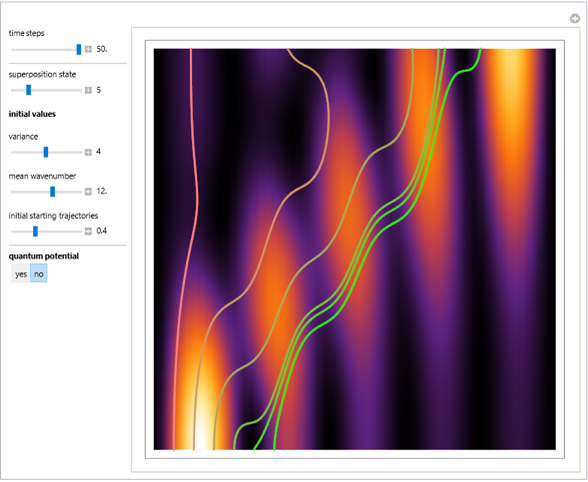In this Demonstration, the particles follow the wave density , which is a solution of the famous Korteweg–de Vries (KdV) equation, and in which a quantum-like potential, here called wave potential or fluid pressure, is responsible for the acceleration or deceleration of the particles. For two very special cases, the dynamics (like trajectories, velocities, acceleration, and density) are given analytically. The waves could be described as a rational solution and a solitary wave of the KdV equation [1]. It is notable that a fluid pressure, which likely has the same form as the quantum potential in the causal interpretation, appears in the acceleration term of the KdV equation, which of course introduces highly non-Newtonian behavior. The "wave potential" differs slightly in the definition. Here, it is a nonlinear function of the density itself. But as in the causal interpretation, the effect of the quantum-like potential varies with the form of the wave function and not its intensity. The potential acts instantaneously and does not diminish as the distance between two particles increases. The time evolution of the position could be interpreted as streamlines of the wave or as idealized test particles that do not interact on each other and do not perturb the wave. The graphic on the left shows the density (black), the quantum potential (red), and the acceleration (blue). On the right, you can see the contours and the trajectories in -space.