Shell Space: Flare, Verm, and Spire

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
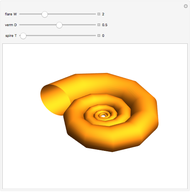
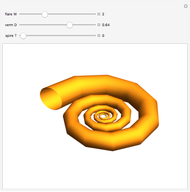
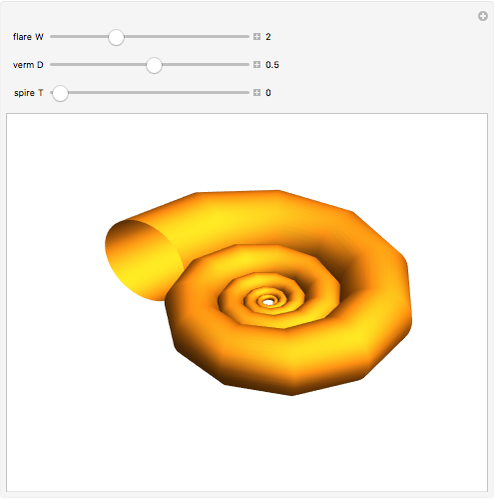
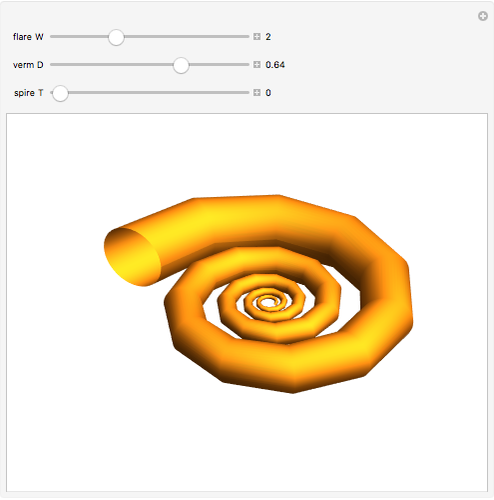
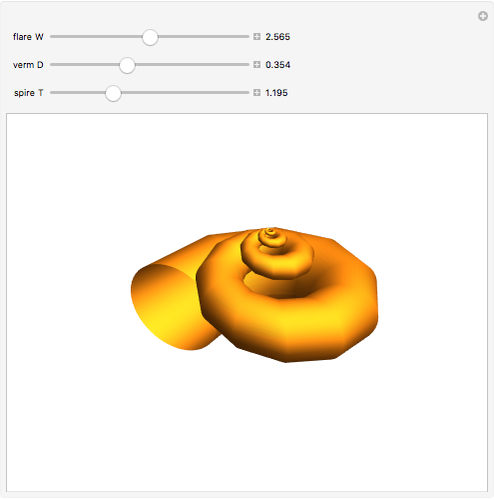
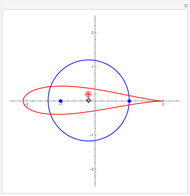
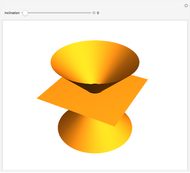
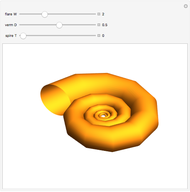
This resembles Stephen Wolfram's model of shell growth. However, this is an implementation of a simpler model, due to David Raup and later used by Richard Dawkins in an influential popularization. The idea is that all naturally occurring shells conform to the same basic design, varying only in a limited number of quantifiable ways. In this model, you can specify a shell by setting the flare, 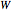 (the rate of growth of the spiral), the verm,
(the rate of growth of the spiral), the verm, 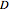 (the "tightness" of the shell cavity), and the spire,
(the "tightness" of the shell cavity), and the spire, 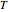 (the rate of creep parallel to the spiral axis).
(the rate of creep parallel to the spiral axis).
Contributed by: Phil Ramsden (March 2011)
Open content licensed under CC BY-NC-SA
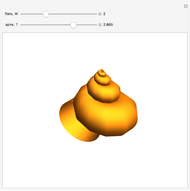
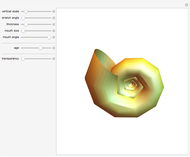
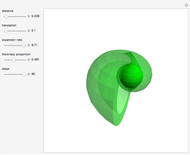
Snapshots
Details
David Raup proposes a simple three-parameter "shell space," the parameters being 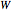 (the rate of growth of the spiral),
(the rate of growth of the spiral), 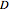 (the "tightness" of the shell cavity), and
(the "tightness" of the shell cavity), and 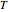 (the rate of creep parallel to the spiral axis).
(the rate of creep parallel to the spiral axis).
This simplified model of "shell space" was later adopted by Dawkins, who coined the terms "flare," "verm," and "spire" for the parameters 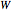 ,
, 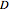 and
and 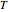 , respectively, as an illustration of the notion of "design space" in the book Climbing Mount Improbable.
, respectively, as an illustration of the notion of "design space" in the book Climbing Mount Improbable.
Here are precise definitions of the parameters.
1. If 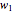 is the distance between a point
is the distance between a point 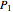 on the generating spiral and that spiral's axis, and
on the generating spiral and that spiral's axis, and 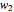 the distance from the corresponding point
the distance from the corresponding point 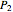 one turn later, then
one turn later, then 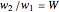 , which is strictly greater than 1.
2. If
, which is strictly greater than 1.
2. If 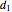 is the distance between the spiral axis and the inner edge of the shell cavity, and
is the distance between the spiral axis and the inner edge of the shell cavity, and 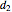 the distance between the spiral axis and the outer edge on the same turn, then
the distance between the spiral axis and the outer edge on the same turn, then 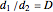 , which is greater than or equal to 0 and strictly less than 1.
3. If the acute angle between the line
, which is greater than or equal to 0 and strictly less than 1.
3. If the acute angle between the line 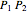 and the horizontal is
and the horizontal is  , then
, then  .
.
Permanent Citation