The Routing Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
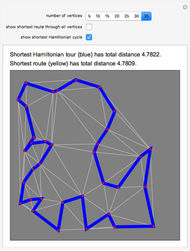
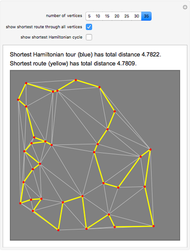
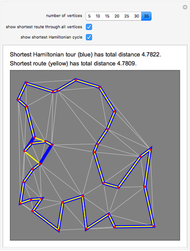
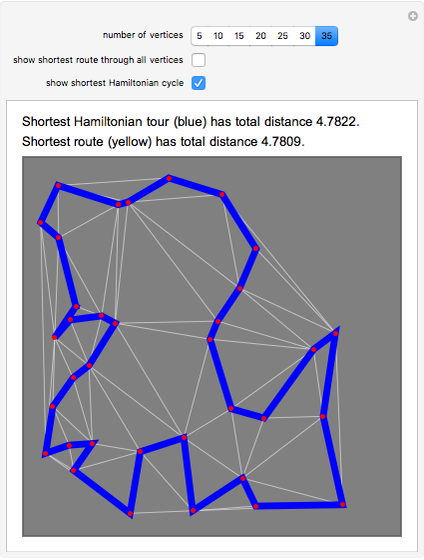
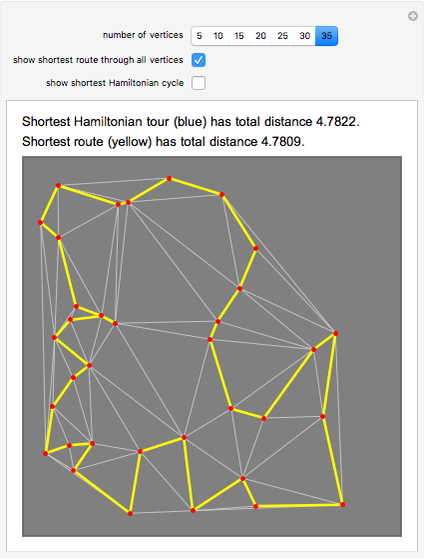
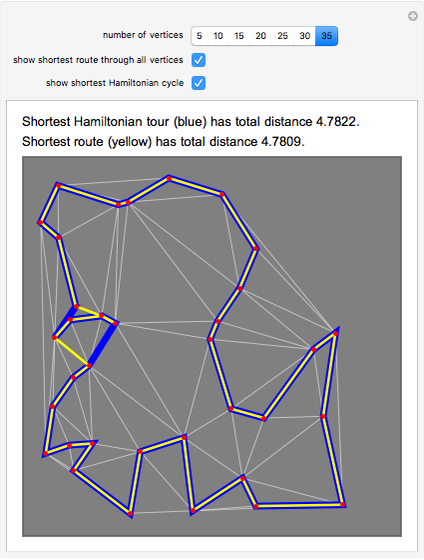
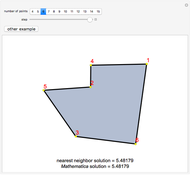
Given a graph, perhaps derived from a map of roads or walkways, a natural problem is to find the shortest cycle in the graph that visits all vertices. This is called the routing problem. A closely related problem is to find the shortest Hamiltonian cycle, where the path visits all vertices but does not repeat any edges. These two problems sound identical, but they are not, since it can happen that backtracking along an edge can lead to a shorter overall route. All distances here are Euclidean distances; the blue cycle is the shortest Hamiltonian tour, and the yellow cycle is the shortest solution to the routing problem.
Contributed by: Stan Wagon (December 2010)
Macalester College
Open content licensed under CC BY-NC-SA
Snapshots
Details
The cases of 30 and 35 vertices show situations where the routing problem has a solution that is better than the shortest Hamiltonian tour. The optimal tours were found by combining integer linear programming with some cycle-breaking, as described in [1] and the Demonstraton "Finding the Shortest Traveling Salesman Tour". A nonedge is an edge in the complement of the graph. For the routing problem, the distance function for nonedges is defined by the shortest-path distance in the graph; any nonedge appearing in the optimal solution is replaced by the corresponding shortest path along edges. It is this replacement that leads to repeated traversal of the same edges.
Reference
[1] S. Wagon, Mathematica in Action, New York: Springer-Verlag, 2010 Chapter 13.
Permanent Citation
"The Routing Problem"
http://demonstrations.wolfram.com/TheRoutingProblem/
Wolfram Demonstrations Project
Published: December 29 2010