Simplified Social Amoebae

Being able to provide clues to the development and evolution of all living things, social amoebae [1], or cellular slime molds, have been widely studied for decades, as they can form a multicellular organism that has a remarkable ability to move and orient itself in its environment while maintaining a sophisticated division of labor. A vivid description of cellular slime molds is presented in the review of the book [1] by Danny Yee: "Cellular slime molds are single celled amoebae that live in the soil, where they eat bacteria and reproduce by fission like other amoebae. When they run out of food, however, they aggregate into large 'slugs' which crawl upwards to the soil surface, where they develop into fruiting bodies with spores raised above the ground on a stalk, for dispersal by animals." Such collective behavior (see the movie made by [2]) has been attracting constant attention for many years [2, 3].

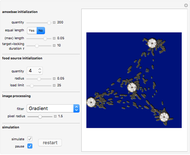
In this Demonstration we do not yet intend to simulate the sophisticated collective behavior of social amoebae, but present some simplified behavior. The algorithm is described in the following steps.

1. At the beginning, amoebae with length and nFS food sources with radius will be distributed at random within a square region with side length 1. Food sources are fixed; as there is a fixed minimum distance among them, it is not recommended to set the quantity of food source too high if you would like to modify the code. All amoebae will try to move to link to a food source but their movement will not cross the region's boundaries during simulation. Once an amoeba links to a food source it will stop moving and become a fixed amoeba. A fixed amoeba can act as a tube and transport food to other amoebae that link with it. However, food sources have a load limit , so only up to amoebae can link to a food source. When this limit is reached, any new requests of amoebae for linking to this food source will be rejected. Amoebae have unlimited lifetime.

2. Any amoeba can link to a food source by a direct link or indirect link. A direct link refers to the case when the distance between the center of a food source and the center of an amoeba satisfies ; whereas an indirect link refers to the case when but there is at least one fixed amoeba and the distance between the centers of these two amoebae satisfies , where is a parameter and it is set to 0.8 in this Demonstration.

3. Every amoeba has the special ability that at each step it can sense the approximate positions of all food sources. That is, if a food source is located at , then an amoeba will sense its position as (,), where both and are pseudorandom variates from the normal distributions and . We call these sensed positions virtual targets.

4. When the simulation starts, each amoeba can sense virtual targets. The probability that the virtual target being chosen by as its actual target that it will move toward at this step is determined by the distances between the and the virtual targets, namely,

(1) .

So the nearer the virtual target, the higher probability it has to be chosen. As the simulation continues, some food sources may become fully loaded. If food source is fully loaded and an unfixed amoeba comes to link to it, then will be rejected. Every amoeba has its own memory (a rejection record) that records the times it has been rejected by every food source. Therefore, if is rejected by then at the next step the probability that still chooses as its actual target will be halved,

(2) ,

where denotes the number of times that has been rejected by . Supposing that of the food sources are fully loaded, then the probability that amoeba will choose a different food source as its actual target is determined by

(3) .

Equations (2) and (3) ensure that after a few repeated rejections by food source and after the completion of the current -step process (see step 5), amoeba will then leave and try to link to other food sources, even though it is actually in the vicinity of . If amoeba records that it has been rejected by all food sources, then all its probabilities will be determined by equation (2) (in this case we need to re-normalize the calculated probabilities so that for any we have ).

5. Once a virtual target is chosen by an amoeba, it will lock its attention on this specific food source that is related to the chosen virtual target for steps. In other words, during the next steps this amoeba will keep sensing and moving toward the approximate position (which may still be different at different steps) of this food source only, paying no attention to other food sources, no matter whether it is rejected by this food source or not. After steps pass, if this amoeba still does not link to any food source, it will repeat steps 4 and 5.

[1] J. T. Bonner, The Social Amoebae: The Biology of Cellular Slime Molds, Princeton, NJ: Princeton University Press, 2009.
[2] T. Gregor, K. Fujimoto, N. Masaki, and S. Sawai, "The Onset of Collective Behavior in Social Amoebae," Science, 328, 2010 pp. 1021–1025.
[3] C. M. Waters and B. L. Bassler, "Quorum Sensing: Cell-to-Cell Communication in Bacteria," Annual Review of Cell and Developmental Biology, 21, 2005 pp. 319–346.