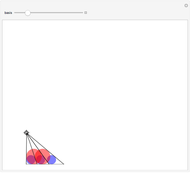
Six Circles Theorem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
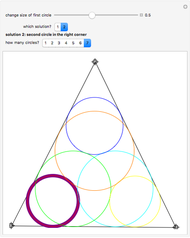
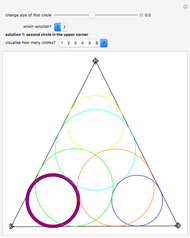
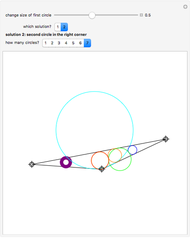
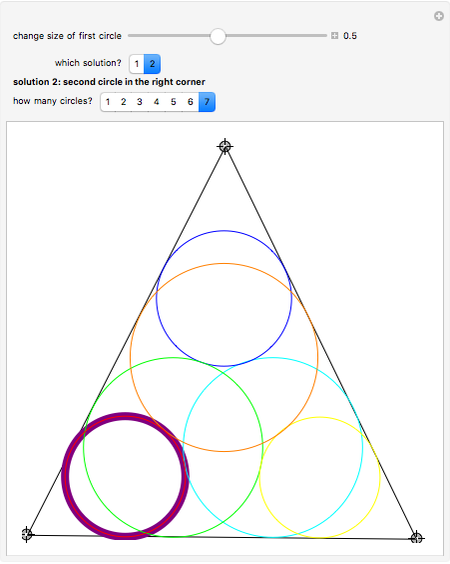
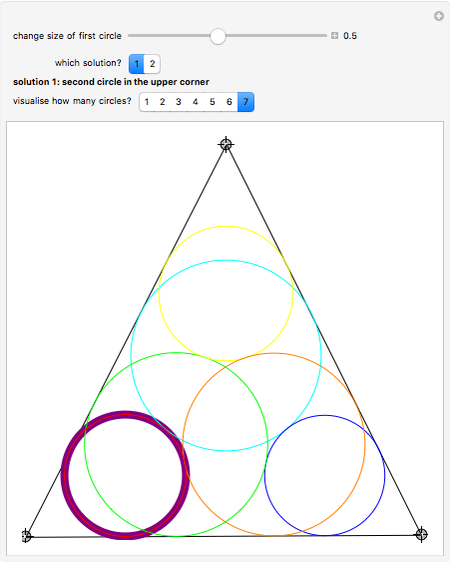
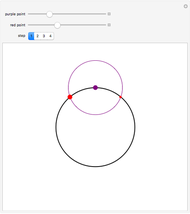
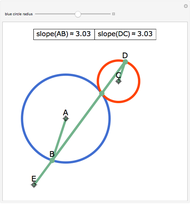
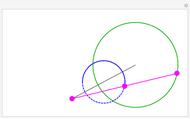
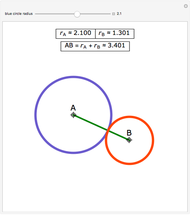
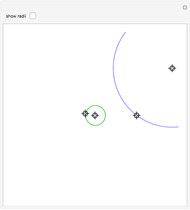
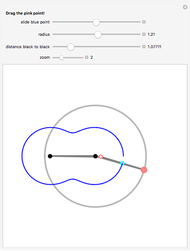
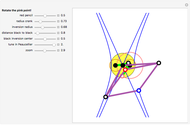
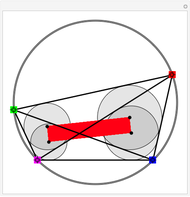
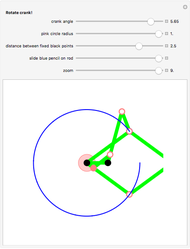
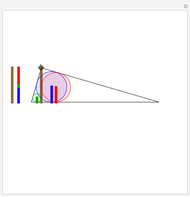
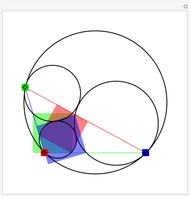
Take a triangle. For each circle tangent to two triangle sides, draw a circle tangent to it and to two sides of the triangle. Iterating the construction you get a circle tangent to the first circle after six steps.
[more]
Contributed by: Claude Fabre (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
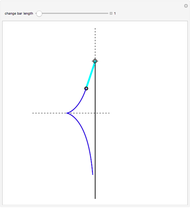
The construction of a circle tangent to two intersecting lines and another circle is not trivial. One has to find the intersection of the bisector and the parabola with focus the center of the first circle. So it seems there is no geometric construction. Therefore we present the analytical construction here. This might explain why this quite instructive theorem was found so late.
C. J. A. Evelyn, G. B. Money-Coutts, J. A. Tyrrell, The Seven Circles Theorem and Other New Theorems, London: Stacey International, 1974 pp. 31–42. (This booklet seems hard to find according to Seven Circles Theorem.)
Permanent Citation
"Six Circles Theorem"
http://demonstrations.wolfram.com/SixCirclesTheorem/
Wolfram Demonstrations Project
Published: March 7 2011