Lucas Circles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
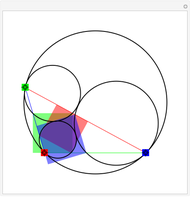
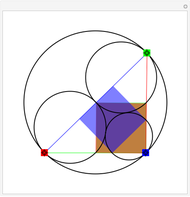
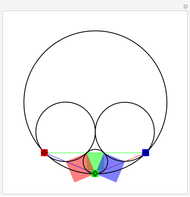
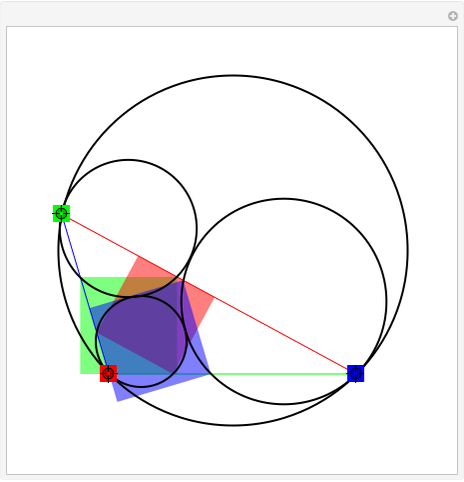
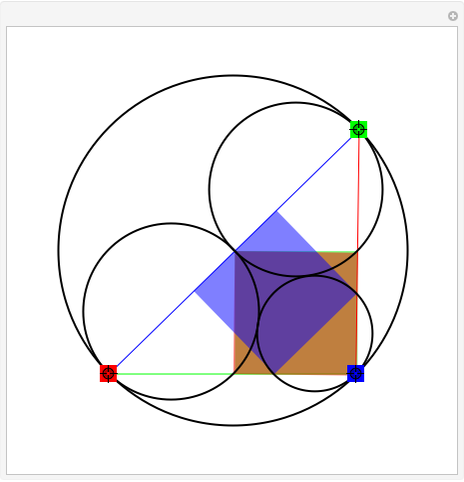
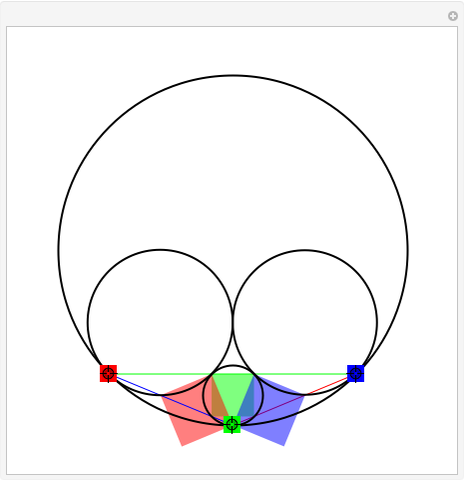
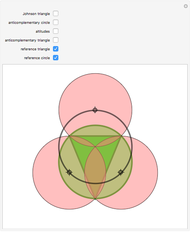
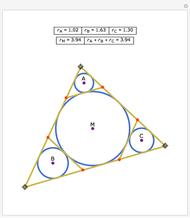
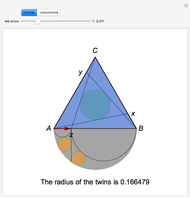
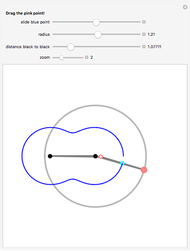
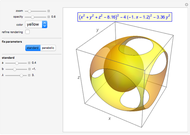
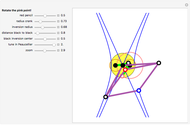
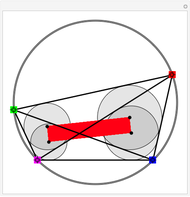
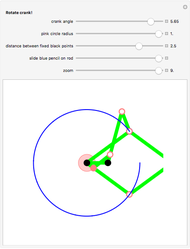
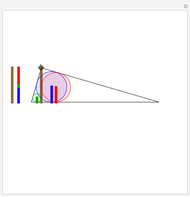
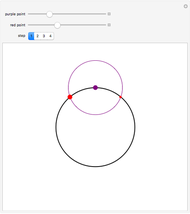
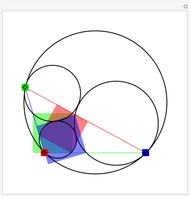
Given a triangle, find three circles that are tangent to the circumcircle of the triangle at the three points and that are also tangent to each other.
[more]
Contributed by: Claude Fabre (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Was Édouard Lucas (1842–1891) the inventor of this gimmick? The problem evokes Descartes's theorem or Soddy circles. Who would think of using these easy-to-construct squares, which apparently do not seem to be related to the problem?
Permanent Citation
"Lucas Circles"
http://demonstrations.wolfram.com/LucasCircles/
Wolfram Demonstrations Project
Published: March 7 2011