Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Families of Figure-Eight Curves

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

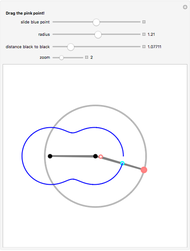
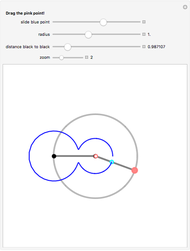
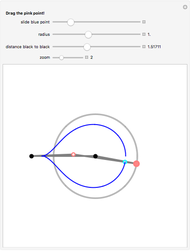
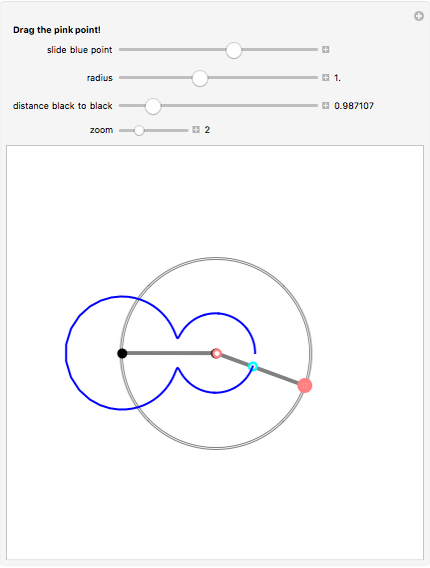
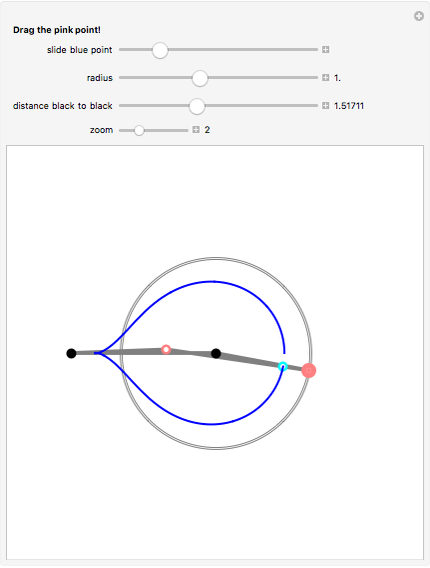
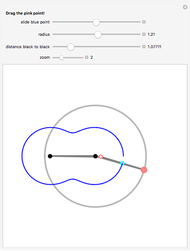
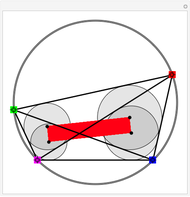
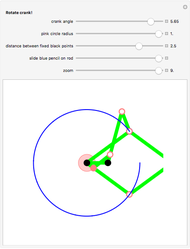
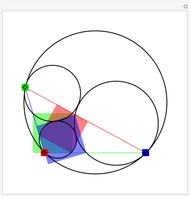
Take a pair of equal short and a pair of equal longer rods. Fix a rod with two nails (here the black points). Let both rods freely rotate around the nails. Hub both free ends together using the remaining fourth rod. Insert a pencil somewhere in this fourth rod (at the cyan point) that will draw the curve.

[more]

As the lengths of the rods and the location of the pencil vary, you get not only the whole Cassini family of curves (including Bernoulli's lemniscate) but also closed asymmetric curves.

[less]

Contributed by: Claude Fabre (September 2009)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The linkage, an isosceles trapezoid (called an isosceles trapezium by the British), shows a very simple mechanism hidden behind curves with complicated Cartesian coordinates. A circular motion gives rise to a large family of curves when throttling the length of the rods.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send