Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

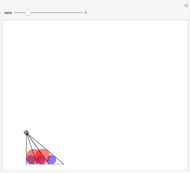
The Conway Circle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

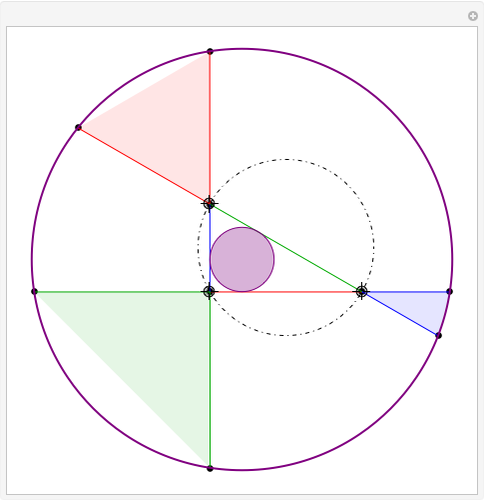
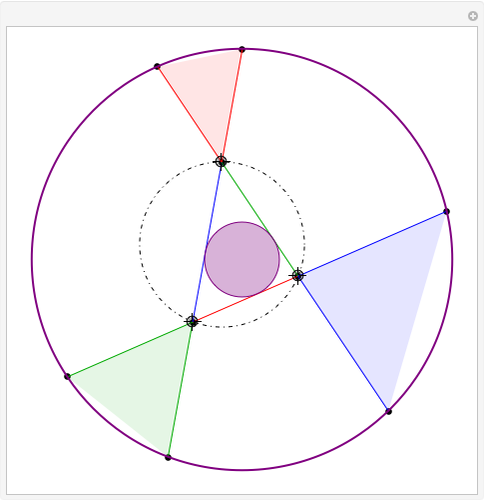
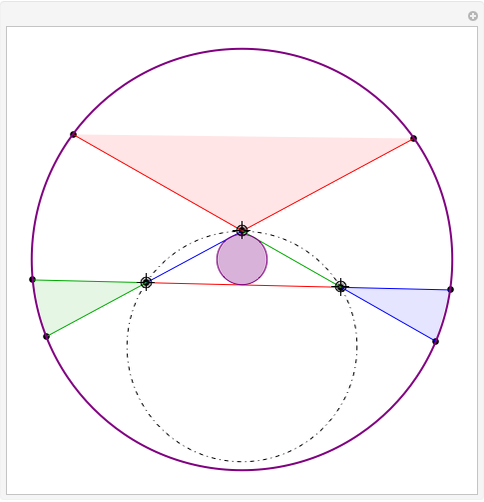
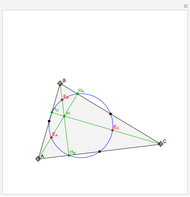
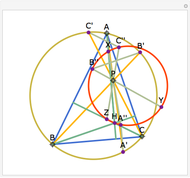
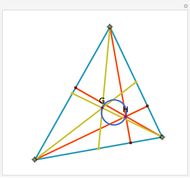
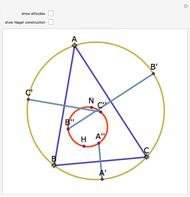
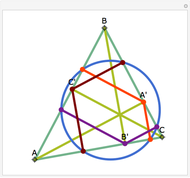
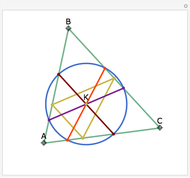
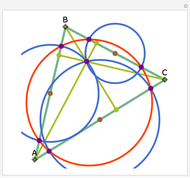
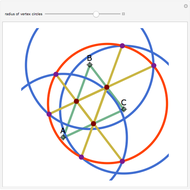
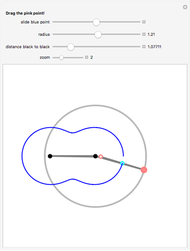
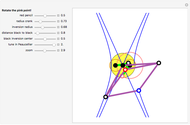
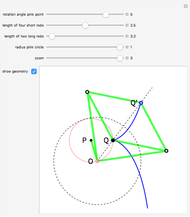
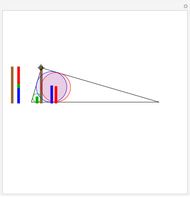
Take a triangle. Extend each side by the lengths of the other two sides, as in the figure where all segments of the same color are equal. Then the endpoints of the extended segments (with length the triangle's perimeter) lie on a circle centered at the incenter.

Contributed by: Claude Fabre (March 2011)
Open content licensed under CC BY-NC-SA

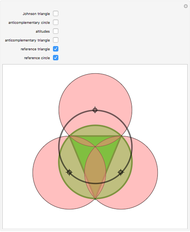
Snapshots

Details

Johnson Horton Conway is not only celebrated for high-ranked results. We also owe him for creating beautiful mathematics made accessible to interested amateurs. His circle is an example. For more information on the other interesting properties, just surf the web.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send