Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

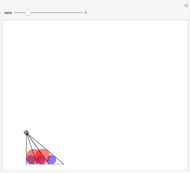
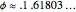Phyllotaxis Explained

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

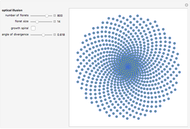
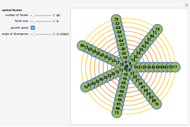
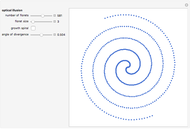
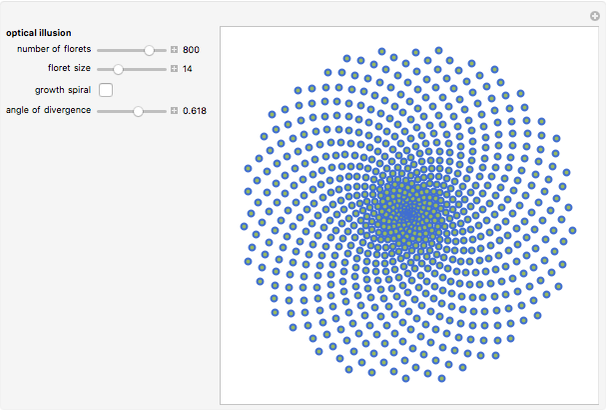
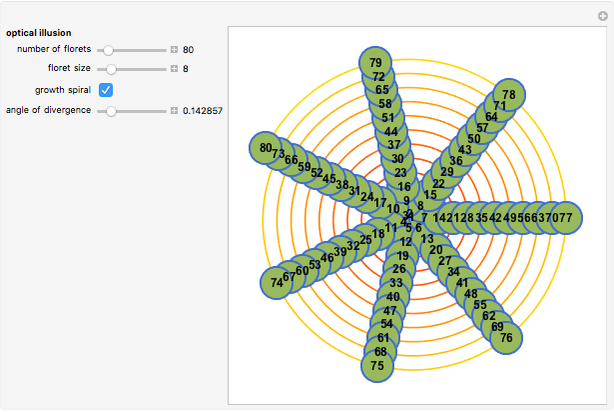
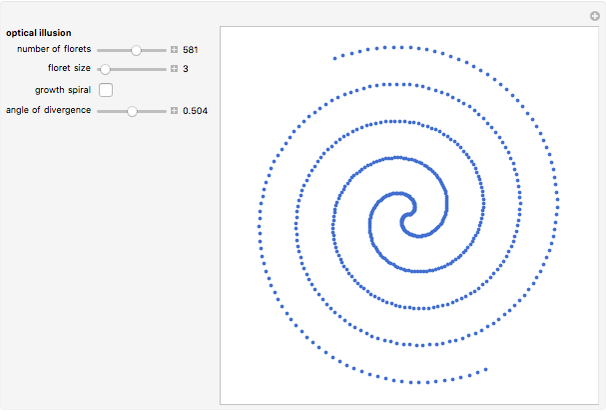
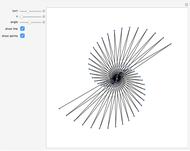
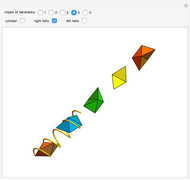
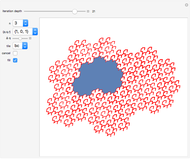
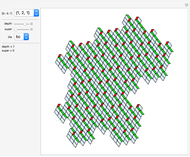
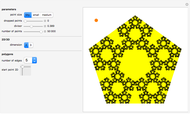
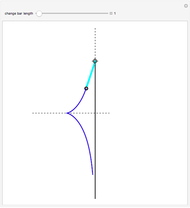
Here is a visual illustration of how the angle of divergence affects the distribution of petals, leaves, florets, and so on in botany.

[more]

In the initial settings, the angle parameter is the inverse of the golden ratio, . Count the number of ghost spirals (parastichies) turning to the left and right. You find two consecutive Fibonacci numbers depending on the number of florets. Unmask this optical illusion by looking at the growth spiral.

Beyond this special golden angle the Demonstration gives all distributions of phyllotaxis. Try irrational and rational numbers for the angle parameter.

[less]

Contributed by: Claude Fabre (July 2010)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The florets are arranged on an Archimedean spiral, according to the simple parametrization 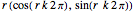, with 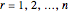and .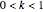

Using 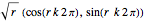would return analogous distributions by maximal packing efficiency, but the growth spiral would no longer be Archimedean.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send