Solving the 2D Helmholtz Partial Differential Equation Using Finite Differences

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
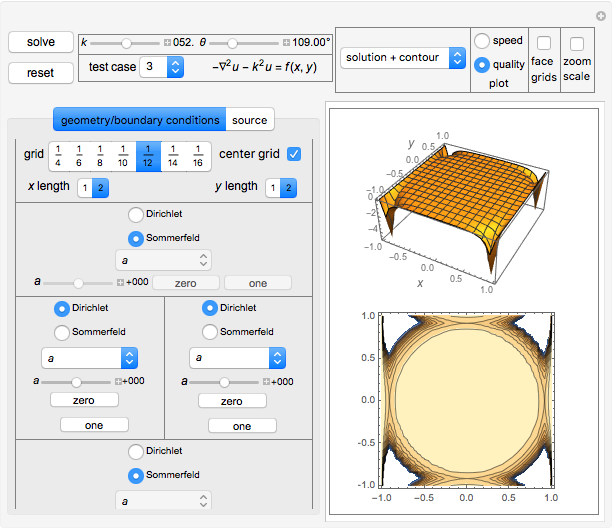
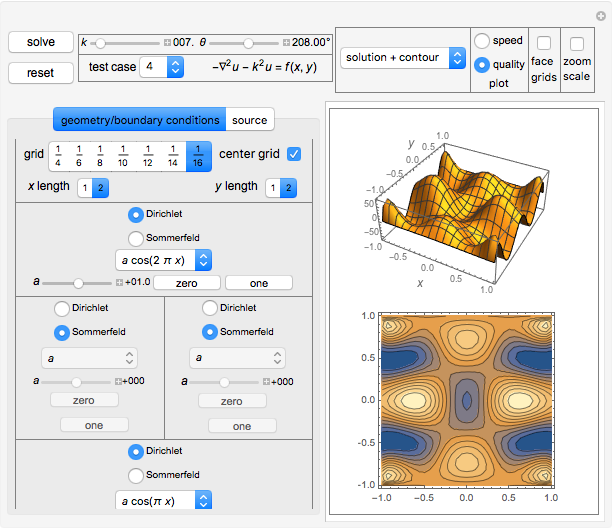
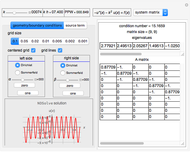
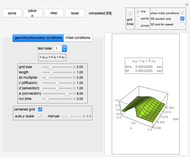
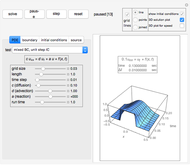
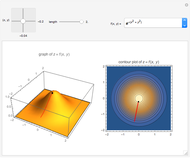
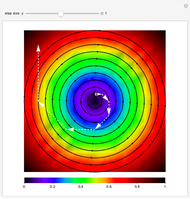
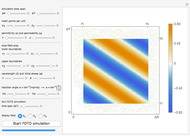
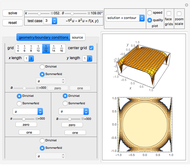
This Demonstration implements a recently published algorithm for an improved finite difference scheme for solving the Helmholtz partial differential equation 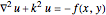 on a rectangle with uniform grid spacing. Dirichlet and Sommerfeld boundary conditions are supported. You can specify different source functions
on a rectangle with uniform grid spacing. Dirichlet and Sommerfeld boundary conditions are supported. You can specify different source functions  . You can prescribe Sommerfeld boundary conditions on up to three edges of the rectangle at the same time. You can vary the
. You can prescribe Sommerfeld boundary conditions on up to three edges of the rectangle at the same time. You can vary the  value and the angle of incidence
value and the angle of incidence  . The numerical scheme is converted to a standard system of linear equations
. The numerical scheme is converted to a standard system of linear equations  system, which can then be solved. You can view the generated matrix
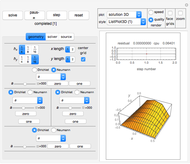
system, which can then be solved. You can view the generated matrix  and its eigenvalues as well as the solution data using the dropdown menu in the top row.
and its eigenvalues as well as the solution data using the dropdown menu in the top row.
Contributed by: Nasser M. Abbasi (June 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Details of the algorithm are described in [1]. This implementation converts the finite difference scheme to the standard  form and uses the built-in Mathematica function LinearSolve to obtain the solution. Sparse matrices are used. The matrix
form and uses the built-in Mathematica function LinearSolve to obtain the solution. Sparse matrices are used. The matrix  and its eigenvalues and the numerical solution
and its eigenvalues and the numerical solution  can be viewed using the dropdown menu. The discretized scheme is given by
can be viewed using the dropdown menu. The discretized scheme is given by  where
where  and
and  .
.
Click the "solve" button after making changes to the UI variables to get a new solution. The "reset" button is used to initialize the system back to the state it was before the "solve" button was clicked. Different types of plots and options are available to choose from.
Reference
[1] Y. S. Wong and G. Li, "Exact Finite Difference Schemes for Solving Helmholtz Equation at Any Wavenumber," International Journal of Numerical Analysis and Modeling, Series B, Computing and Information, 2(1), 2010 pp. 91–108.
Permanent Citation