Solving the 2D Poisson PDE by Eight Different Methods

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
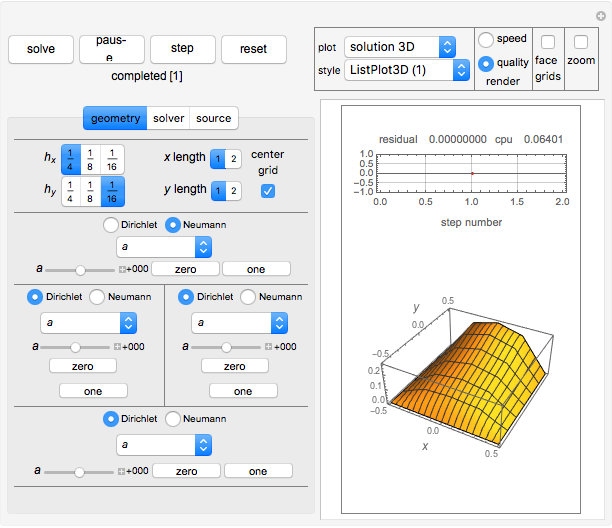
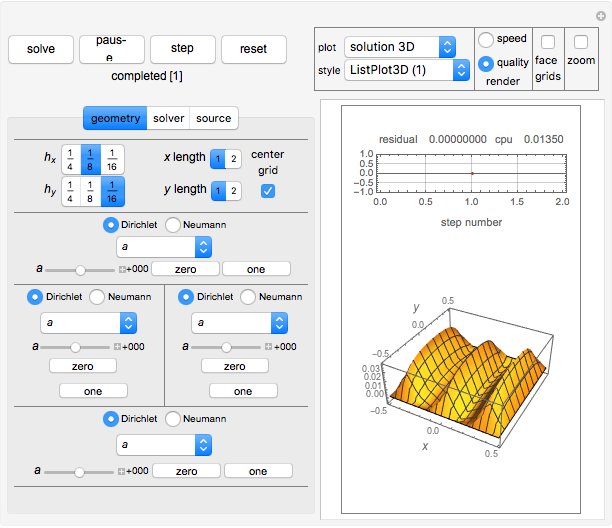
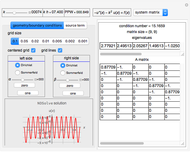
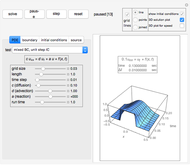
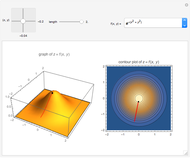
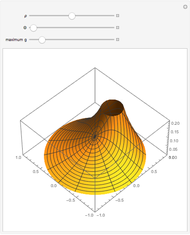
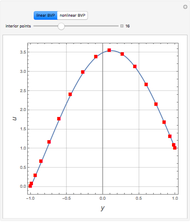
This Demonstration considers solutions of the Poisson elliptic partial differential equation (PDE)  on a rectangular grid. Eight numerical methods are based on either Neumann or Dirichlet boundary conditions and nonuniform grid spacing in the
on a rectangular grid. Eight numerical methods are based on either Neumann or Dirichlet boundary conditions and nonuniform grid spacing in the  and
and  directions. Different source functions
directions. Different source functions  are considered.
are considered.
Contributed by: Nasser M. Abbasi (August 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation
"Solving the 2D Poisson PDE by Eight Different Methods"
http://demonstrations.wolfram.com/SolvingThe2DPoissonPDEByEightDifferentMethods/
Wolfram Demonstrations Project
Published: August 17 2012