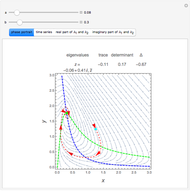
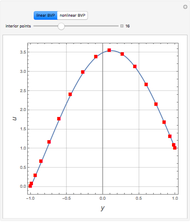
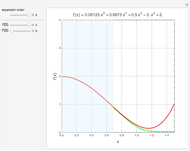
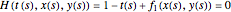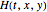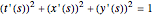All Real Roots of a Nonlinear System of Equations
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
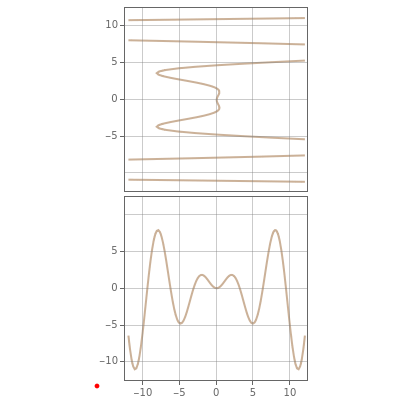
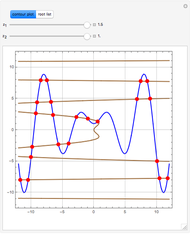
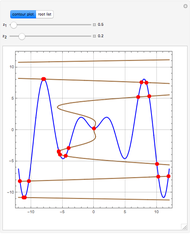
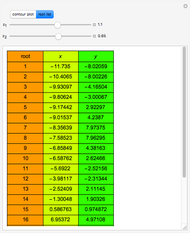
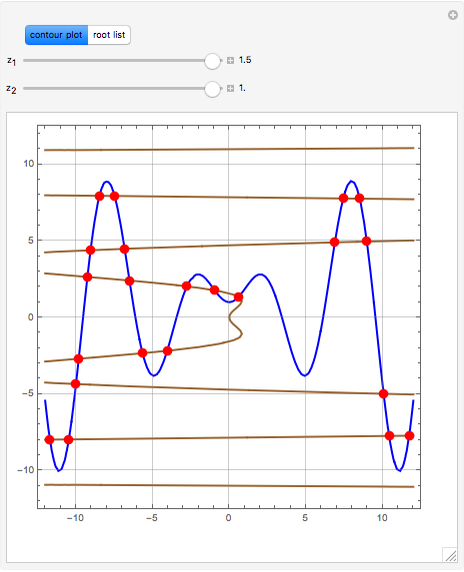
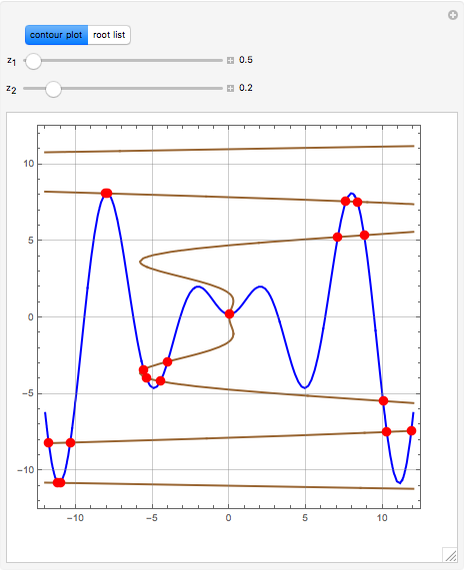
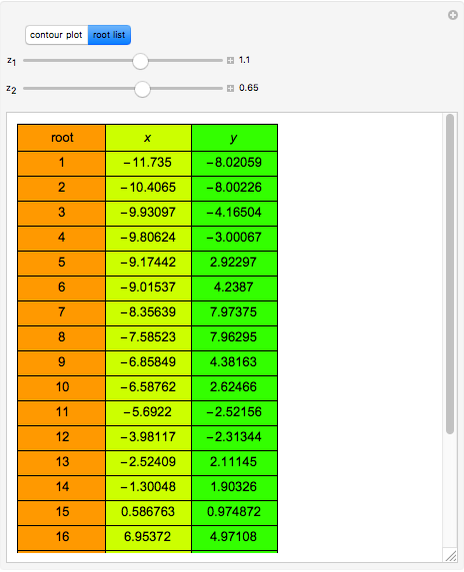
Consider the system of nonlinear algebraic equations: 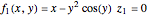 and
and 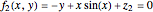 , where you can vary
, where you can vary 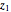 and
and 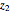 .
.
Contributed by: Housam Binous, Ahmed Bellagi, and Brian G. Higgins (December 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] S. K. Rahimian, F. Jalali, J. D. Seader, and R. E. White, "A New Homotopy for Seeking all Real Roots of a Nonlinear Equation," Computers and Chemical Engineering, 35(3), 2011 pp. 403–411. doi:10.1016/j.compchemeng.2010.04.007.
Permanent Citation