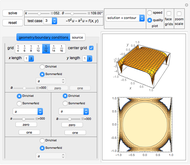
Dynamic Analysis of a Second-Order System with Harmonic Loading

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
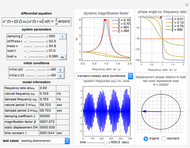
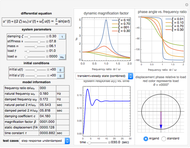
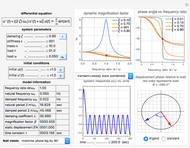
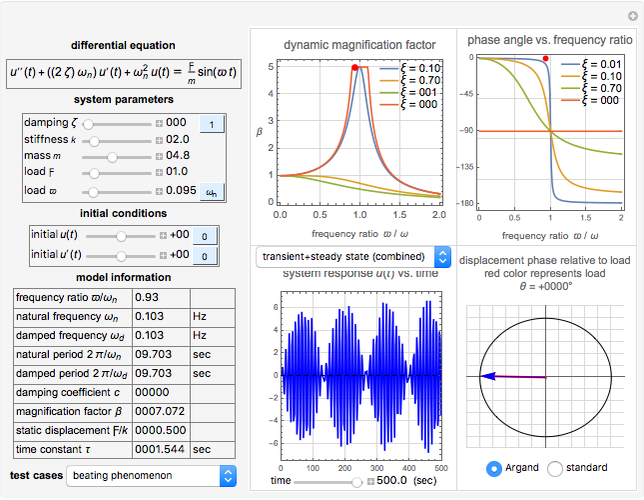
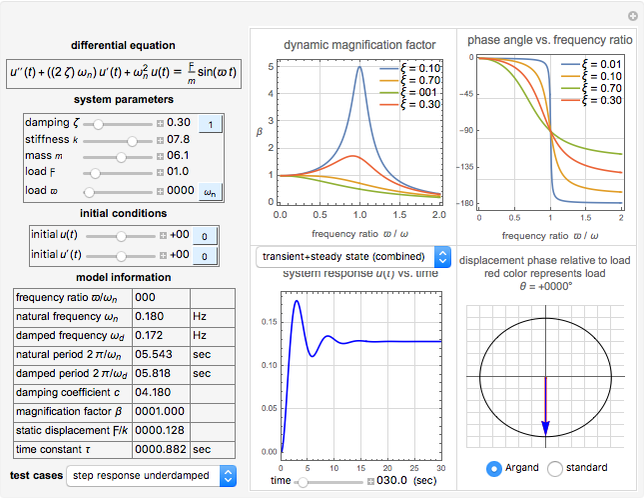
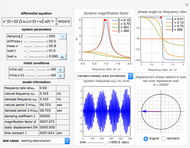
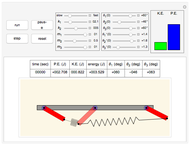
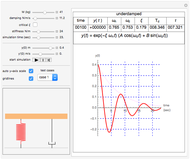
This Demonstration gives a complete analysis of a second-order system with harmonic loading. The system's differential equation is 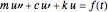 , where
, where 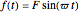 ,
, 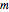 is the mass of the system,
is the mass of the system,  is the damping coefficient,
is the damping coefficient,  is the stiffness,
is the stiffness, 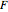 is the magnitude of the force, and
is the magnitude of the force, and 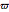 is the force frequency. The response
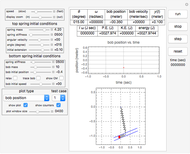
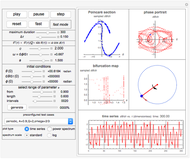
is the force frequency. The response 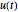 is plotted as a function of time for the underdamped, critically damped, and overdamped cases. This Demonstration displays the transient response (the homogeneous part of the total solution), the steady state response (the particular part of the total solution), and the total response, which is the combination of the two. You can see the analytical solution for each case by moving the mouse over the response curve. Separate displays are given for the dynamic magnification factor and the phase of the response relative to the force. A number of pre-configured test cases can be chosen, to illustrate several important cases of system responses under different loading conditions.
is plotted as a function of time for the underdamped, critically damped, and overdamped cases. This Demonstration displays the transient response (the homogeneous part of the total solution), the steady state response (the particular part of the total solution), and the total response, which is the combination of the two. You can see the analytical solution for each case by moving the mouse over the response curve. Separate displays are given for the dynamic magnification factor and the phase of the response relative to the force. A number of pre-configured test cases can be chosen, to illustrate several important cases of system responses under different loading conditions.
Contributed by: Nasser M. Abbasi (August 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The equation of motion of a second-order linear system of mass 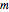 with harmonic applied loading is given by the differential equation
with harmonic applied loading is given by the differential equation 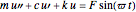 . There are 12 different analytical solutions depending on whether damping or loading is present and, if so, whether the system is underdamped, critically damped or overdamped.
. There are 12 different analytical solutions depending on whether damping or loading is present and, if so, whether the system is underdamped, critically damped or overdamped.
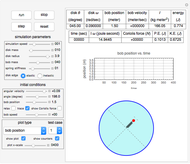
The solution for each of the 12 cases was derived analytically and shown in the Demonstration, subject to the user's choice. Following are definitions of the relevant parameters. All units are in SI.
The damping ratio is 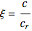 , where
, where  is the damping coefficient, such that
is the damping coefficient, such that 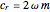 represents critical damping. The natural underdamped frequency is given by
represents critical damping. The natural underdamped frequency is given by 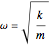 , where
, where  is the stiffness and
is the stiffness and 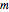 is the mass. The damped frequency of the system, defined for
is the mass. The damped frequency of the system, defined for 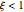 , is
, is 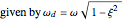 . The frequency ratio is
. The frequency ratio is 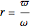 , where
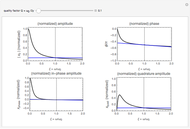
, where 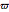 is the forcing frequency. The dynamic magnification factor
is the forcing frequency. The dynamic magnification factor 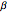 is the ratio of the steady state response to the static response. The static response is given by
is the ratio of the steady state response to the static response. The static response is given by 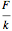 , where
, where 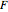 is the force magnitude. The time constant is
is the force magnitude. The time constant is 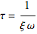 and the damped period of oscillation is
and the damped period of oscillation is 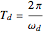 .
.
When the system is undamped and the load is harmonic, resonance occurs when 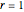 or
or  . When the system is underdamped and the load is again harmonic, practical resonance occurs when
. When the system is underdamped and the load is again harmonic, practical resonance occurs when 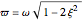 and the corresponding maximum magnification factor is
and the corresponding maximum magnification factor is 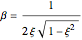 . You can force the loading frequency to be equal to the natural frequency by clicking the button located to the right of the slider used to input the loading frequency. The forcing frequency
. You can force the loading frequency to be equal to the natural frequency by clicking the button located to the right of the slider used to input the loading frequency. The forcing frequency 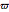 is expressed in Hz, but converted to radians per second internally.
is expressed in Hz, but converted to radians per second internally.
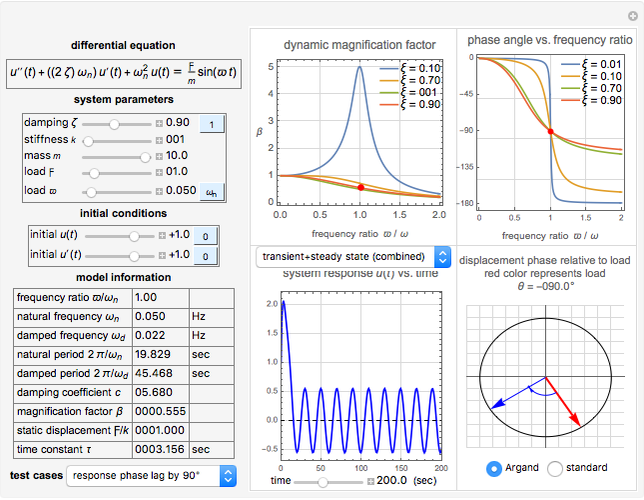
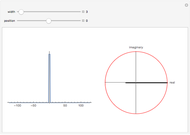
This Demonstration also shows plots of the phase of the response 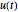 relative to loading
relative to loading 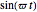 . The phase of the response lags behind loading by an angle
. The phase of the response lags behind loading by an angle 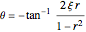 , which is plotted in the complex plane on an Argand diagram. The phase angle ranges from
, which is plotted in the complex plane on an Argand diagram. The phase angle ranges from 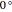 to
to 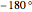 .
.
When the loading frequency 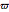 is set to zero, only
is set to zero, only 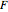 is used as the force
is used as the force 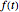 . This allows a constant force loading,
. This allows a constant force loading, 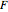 . For example, by setting
. For example, by setting 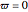 and
and  , a step response is obtained. To make the loading zero, the slider
, a step response is obtained. To make the loading zero, the slider 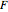 is set equal to zero.
is set equal to zero.
The Demonstration contains a number of pre-configured test cases to illustrate different loading conditions, such as beating phenomenon, resonance, practical response, impulse response, and step responses for different damping values.
References
[1] M. Paz and W. Leigh, Structural Dynamics: Theory and Computation, 5th ed., Boston: Kluwer Academic Publishers, 2004.
[2] W. T. Thomson, Theory of Vibration with Applications, Englewood Cliffs, NJ: Prentice-Hall, 1972.
[3] R. W. Clough and J. Penzien, Dynamics of Structures, New York: McGraw-Hill, 1975.
[4] R. K. Vierck, Vibration Analysis, Scranton, PA: International Textbook Company, 1967.
[5] A. A. Shabana, Theory of Vibration, Vol. 1, New York: Springer-Verlag, 1991.
[6] B. Morrill, Mechanical Vibrations, New York: Ronald Press, 1957.
Permanent Citation