Solid Pendulum with a Spring-Mass System

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
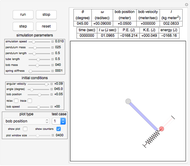
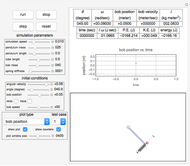
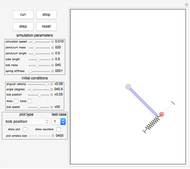
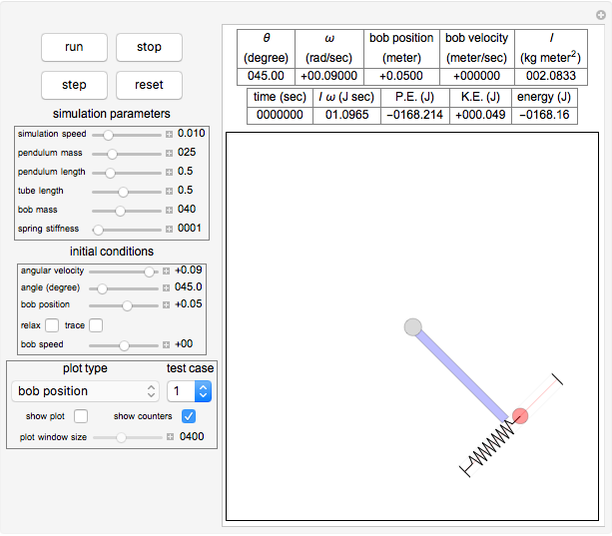
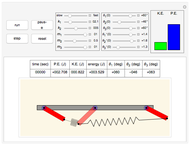
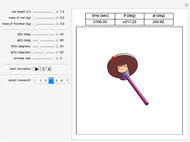
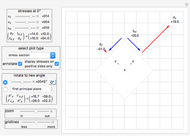
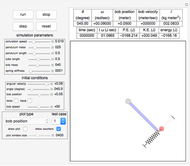
This Demonstration describes the dynamics of a solid pendulum in which a massive bob slides back and forth over a massless and smooth thin tube attached to the bottom of a pendulum bar. The bob is attached to the end of a spring. When the bob hits the ends of the tube, it bounces back; the ends are assumed to be perfectly elastic. The two equations of motion for the bob and the pendulum bar are derived using the Lagrangian method, which is solved numerically by Mathematica's built-in function NDSolve. The spring is anchored to the left edge of the tube, assumed to be massless, and can move in only one direction along the length of the tube. Setting the spring stiffness to zero effectively removes the spring, allowing the bob to oscillate freely.
Contributed by: Nasser M. Abbasi (September 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Description of the User Interface
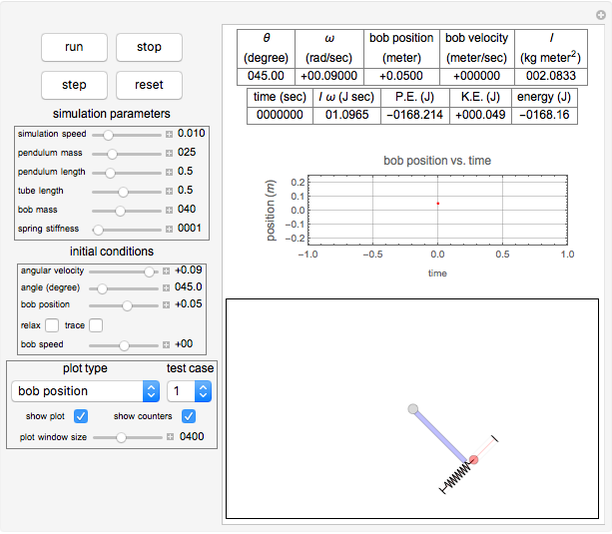
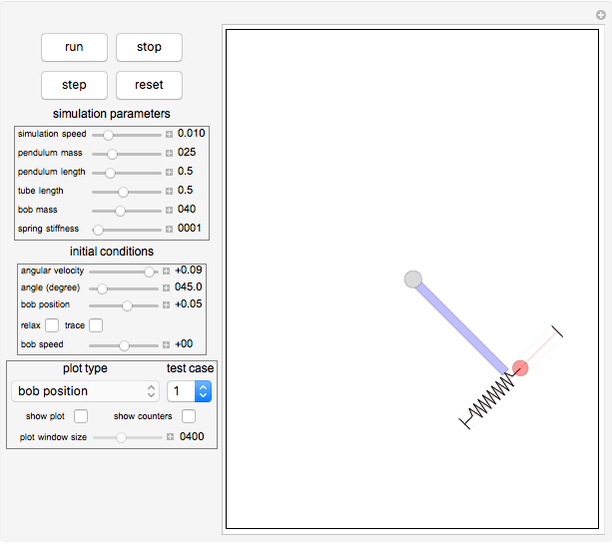
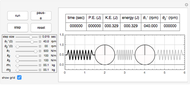
The top four buttons control the Demonstration. The "reset" button brings the simulation back to the initial conditions. The control variables below these buttons are used to change the initial conditions for the pendulum and the bob. The "relax" checkbox is used to put the spring into the relaxed initial position, which is at half the length of the tube. You can see a trace of the bob motion using the "trace" checkbox. You can change the length of the pendulum bar and the tube length as well as their masses.
The result has three parts. The counters at the top show the current state. The field labeled "energy" is the sum of the potential energy (P.E.) and the kinetic energy (K.E.). The field labeled "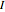 " is the mass moment of inertia of the pendulum bar, defined as
" is the mass moment of inertia of the pendulum bar, defined as 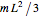 , where
, where 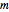 is the mass of the pendulum bar and
is the mass of the pendulum bar and 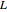 is the length of the bar. The field labeled
is the length of the bar. The field labeled 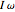 is the total angular momentum of the system. The middle part of the display shows different plots. The plot shown is selected using the popup menu labeled "plot type". The third part shows the pendulum itself as it swings. You can select the parts to see using the checkboxes to the left.
is the total angular momentum of the system. The middle part of the display shows different plots. The plot shown is selected using the popup menu labeled "plot type". The third part shows the pendulum itself as it swings. You can select the parts to see using the checkboxes to the left.
A popup menu labeled "test case" is used to select one of three preconfigured simulation parameters. Click the "run" button after selecting a test case to start the Demonstration.
The Demonstration runs with no throttling by using a single dynamic variable called "gTick" that is updated (or ticked) at the end of each Manipulate expression evaluation, so that the Manipulate expression is reevaluated again immediately. This lets the Demonstration run at the maximum speed. You can use the slider labeled "simulation speed" to adjust the speed of the simulation as desired.
The action runs continuously until you stop it. The time counter rewinds each 1000 seconds. All units are expressed in SI.
Derivation of Equations of Motion
The equations of motion are derived using the Lagrangian method. The bob has one degree of freedom: the distance  along the length of the tube;
along the length of the tube;  is the middle of the tube, which is also the point where the pendulum bar is attached to the tube. The pendulum likewise has one degree of freedom: the angle of rotation
is the middle of the tube, which is also the point where the pendulum bar is attached to the tube. The pendulum likewise has one degree of freedom: the angle of rotation  . For more information on the derivation of the equations of motion, please see the author's report.
. For more information on the derivation of the equations of motion, please see the author's report.
References
[1] D. Morin, Introduction to Classical Mechanics: With Problems and Solutions, New York: Cambridge University Press, 2008.
[2] Research & Education Association, REA Problem Solvers: Mechanics, Piscataway, NJ: Research & Education Association, 2002.
[3] D. A. Wells, Schaum's Outline of Lagrangian Dynamics, New York: McGraw-Hill, 1967.
Permanent Citation