Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Steffen's Flexible Polyhedron

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

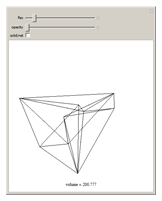
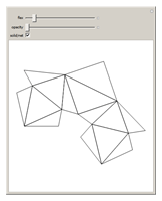
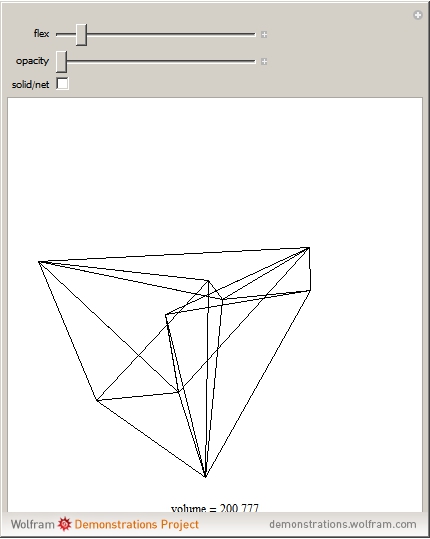
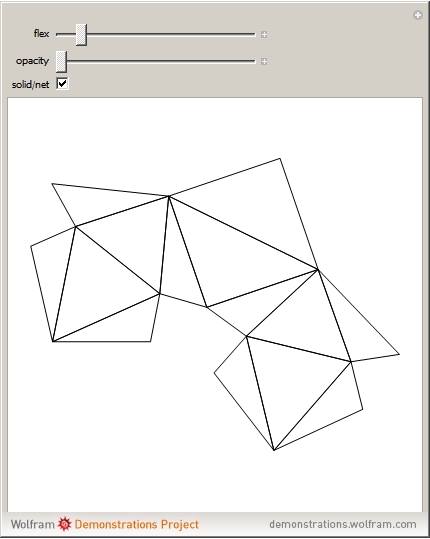
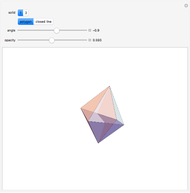
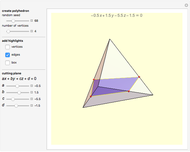
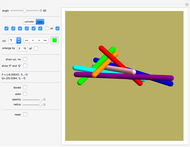
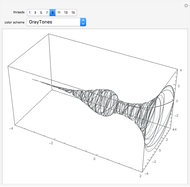
Steffen's polyhedron is able to flex without self-intersection and without distorting any of its faces. It has 14 triangular faces, 21 edges, and 9 vertices. Euler had conjectured no polyhedron could flex. Cauchy proved that convex polyhedra cannot flex.

[more]

The bellows conjecture (proven in 1997) asserts that a flexible polyhedron has constant volume as it is flexed.

[less]

Contributed by: Mark McClure (April 2007)
With additional contribution by Izidor Hafner.
Open content licensed under CC BY-NC-SA

Snapshots

Details

R. Connelly, I. Sabitov, and A. Walz, "The Bellows Conjecture," Contrib. Algebra Geom. 38, pp. 1–10, 1997.

Reference

[1] P. R. Cromwell, Polyhedra, New York: Cambridge University Press, pp. 245 and 247, 1997.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send