Instability of Laplace's Equation

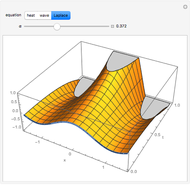
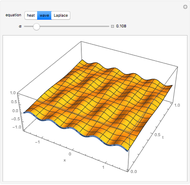
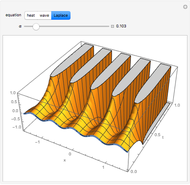
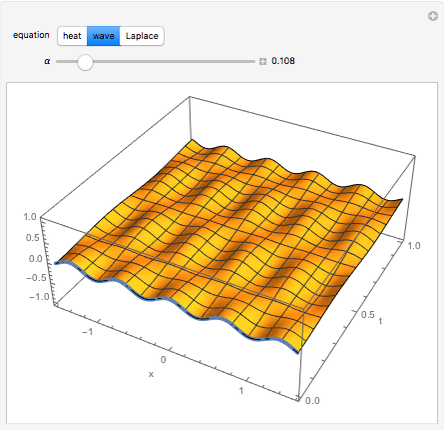
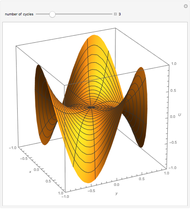
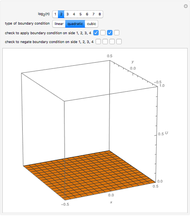
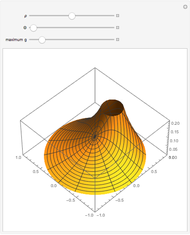
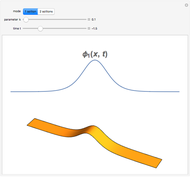
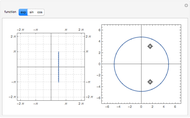
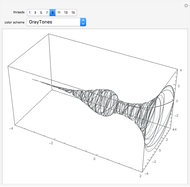
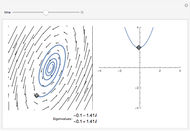
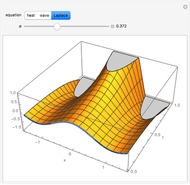
Initial value problems involving the heat and wave equations enjoy a level of stability that Laplace's equation does not. The solution surface for each of these equations is shown for the initial condition 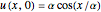. For close to zero, the initial condition function is close to zero and the entire graphs for both the heat and wave equations are close to zero. The solution to Laplace's equation oscillates wildly, however. This is why boundary conditions, rather than initial conditions, are almost always applied to Laplace's equation.