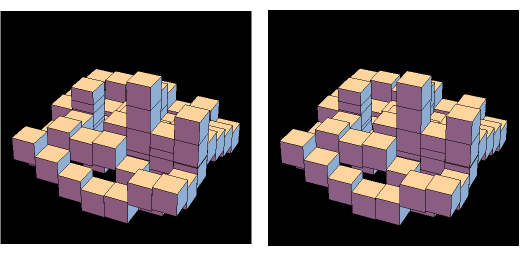
Stereo View without Glasses

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
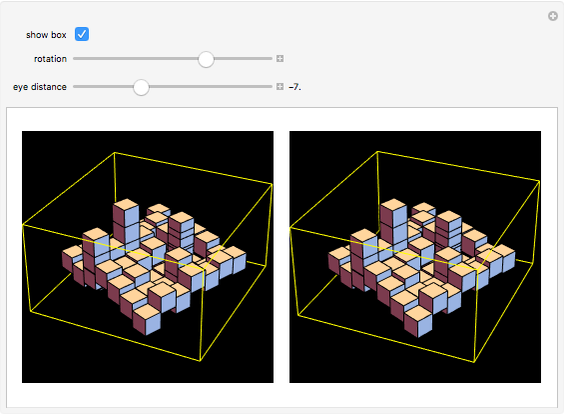
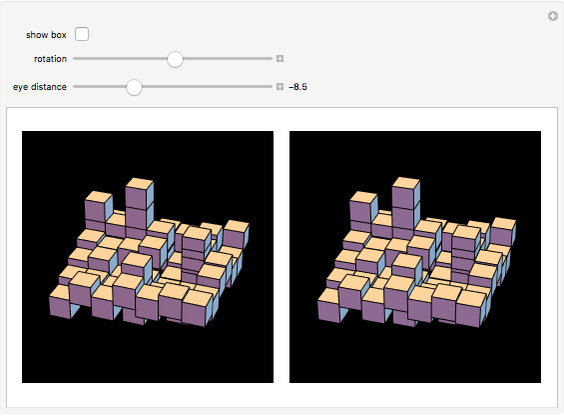
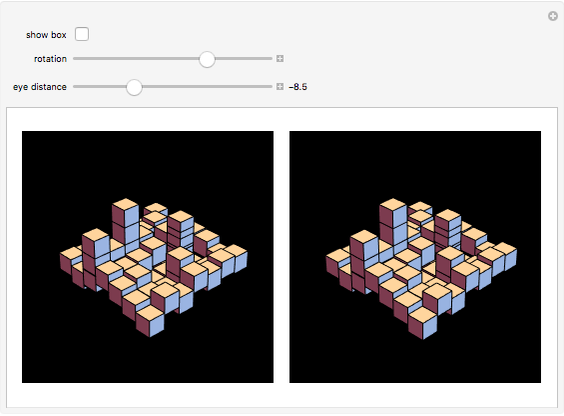
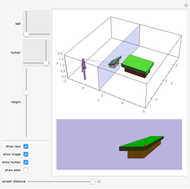
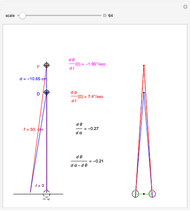
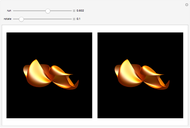
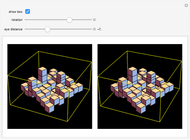
There are several technical methods to make realistic three-dimensional images. Spatial vision is based on the fact that the eyes receive two clearly different perspective pictures. The brain calculates the angle between the two directions to the object to realize the depth effect in our imaginations. Two perspectively correlated pictures are easy to produce with the help of a camera or computer graphics. The problem is to present the images to each eye separately. Two ways to achieve this are red/green glasses and polarized glasses. But the method of cross-view rays is a simple trick to achieve a real 3D impression without glasses. The images are arranged so that the one for the right eye is on the left and vice versa. You must squint so that the right eye looks at the left image and the left eye looks at the right image. To do this, look at one finger half the distance between eyes and screen.
Contributed by: Herbert W. Franke (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
With the slider for the eye distance, you can set the best view for your distance to the screen. Negative values correspond to crossing view directions. The position in the middle—eye distance zero—gives parallel view vectors as if viewing the object from a large distance (or more exactly: it corresponds to an infinite distance). You will see the image as flat, but it seems to be suspended at half the distance between your eyes and the screen; the reason is that your eyes are fixed at a point at half the distance to the screen. The angle of the view vector is the basis for the brain to determine the distance. Positive positions of the eye distance slider do not give realistic settings for the visual system.
Permanent Citation
"Stereo View without Glasses"
http://demonstrations.wolfram.com/StereoViewWithoutGlasses/
Wolfram Demonstrations Project
Published: March 7 2011