Is the Golden Ratio Really the Most Beautiful Proportion?
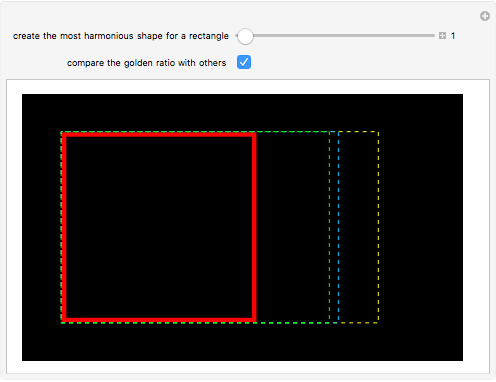
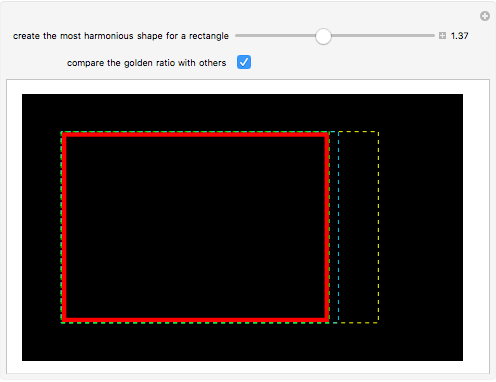
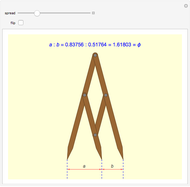
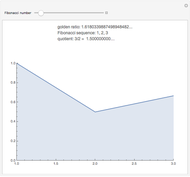
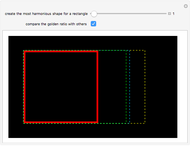
Since the classical age of Greece, the golden ratio has been well known as the most balanced and therefore most aesthetically perfect proportion. In fact, it is supposedly often found in the fine arts and architecture and it is certainly important in geometry. But where is the proof that it is really the most beautiful proportion? For example, could a different value be derived on the basis of information psychology?
This Demonstration allows you to make your own contribution to this question. Use the slider to realize the most harmonic rectangle from your point of view. Then you might find some examples from art or science and make a comparison.
The yellow rectangle has sides whose ratio is the golden ratio . The sides of the blue rectangle are in the proportion , which the German physicist Georg Christoph Lichtenberg designated in 1796 as the most beautiful geometric ratio (Zerbe and Davidshofer, see references). Finally, the green rectangle should have the best proportions, according to a result from information psychology.
The computer is proving to be a useful tool in exact art theory. Works of computer art are produced with the help of programs that describe the logic of the construction and its relevant measures. By varying the parameters you can vary the shapes of objects, and on the basis of the reaction of the public you can determine the best option. So it is possible to find valid rules to design works of art. This Demonstration on the golden ratio is a simple example; it should help to confirm or refute a previously often used but unverified rule for art.
A statistical evaluation would be interesting. Please email me with your results for the optimal proportion at franke@zi.biologie.uni-muenchen.de.
References:
H. Frank, "Grundlagenprobleme der Informationsästhetik und erste Anwendung auf die mime pure," Dissertation, Technische Hochschule Stuttgart, 1959.
W. Zerbe and L. Davidshofer, Satztechnik und Gestaltung: Schweizerisches Fach- und Lehrbuch für Schriftsetzer, Zürich: Bildungsverband Schweizerischer Buchdrucker, 1952.
J. F. Schopp, "Papierformate: Die DIN-Reihe," Universität Tampere (Finnland) 2002 (2. Version; 1. Vers.1998), New Edition: 4. 9. 2002 http://www.uta.fi/~trjusc/dinform.htm
H. Walser, Der Goldene Schnitt, Stuttgart–Leipzig: B. G. Teubner Verlagsgesellschaft and Zürich: Verlag der Fachvereine, 1993.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
