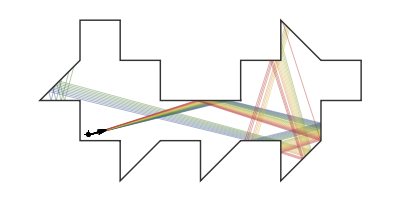The 26-Sided Unilluminable Room

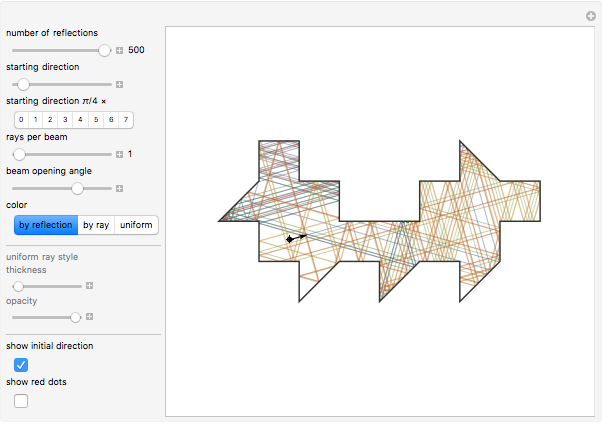
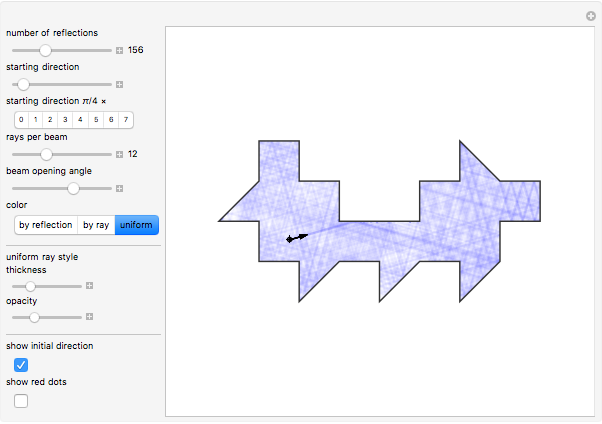
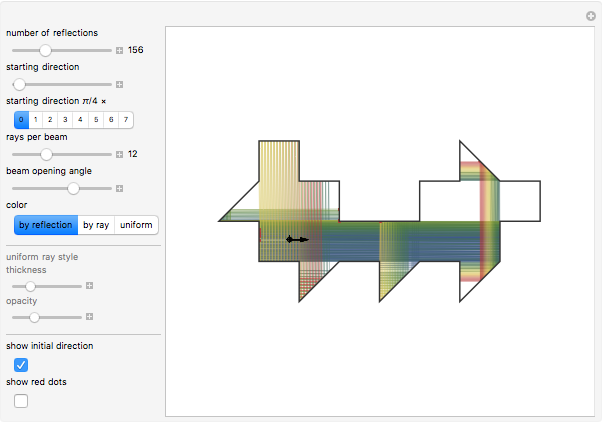
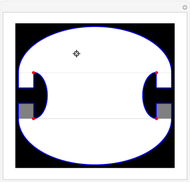
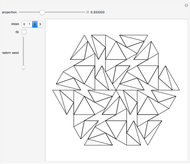
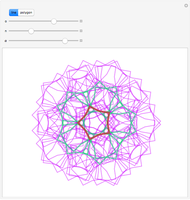
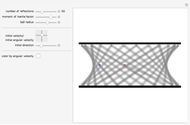
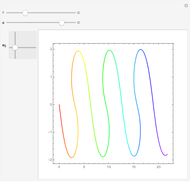
If a candle is inside a room with mirrored walls, can any portion of the room be dark? In 1958, a young Roger Penrose found an unilluminable room with elliptical sides. In 1995, George Tokarsky proved that a light ray starting from one corner of a mirrored 45 degree triangle could never return to that corner. From that, he built a 26-sided room such that a single point of light would lead to a single point of darkness elsewhere in the room. The red dots are a pair of points that theoretically cannot illuminate each other.