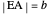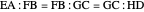Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Eratosthenes Machine for Finding the Cube Root of Two

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

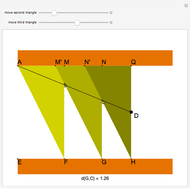
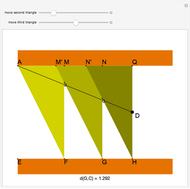
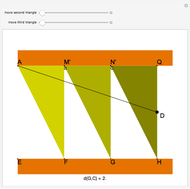
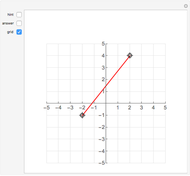
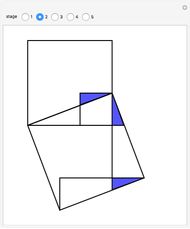
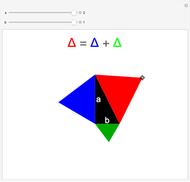
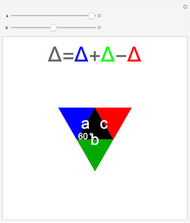
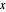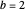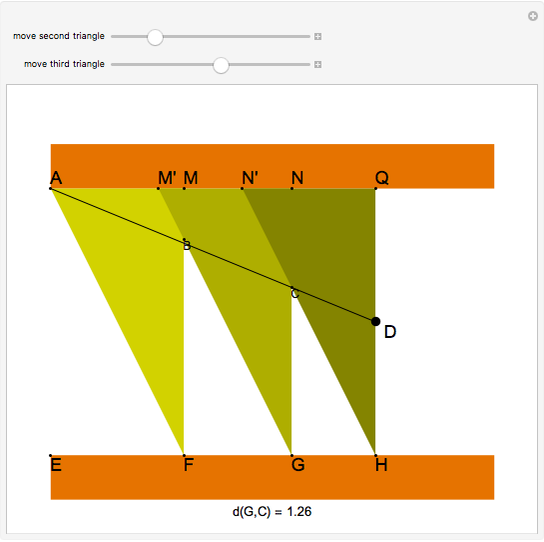
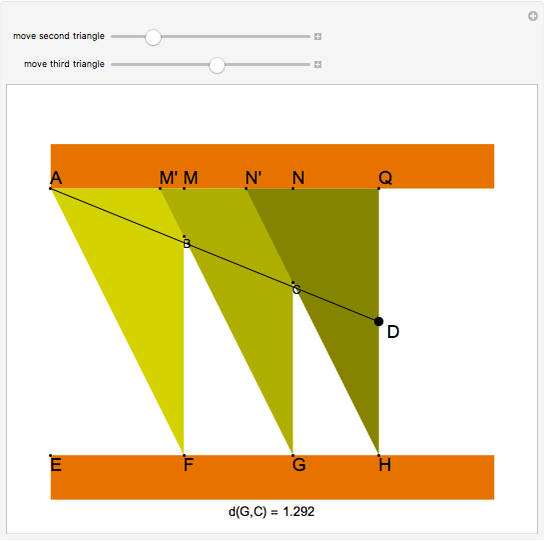
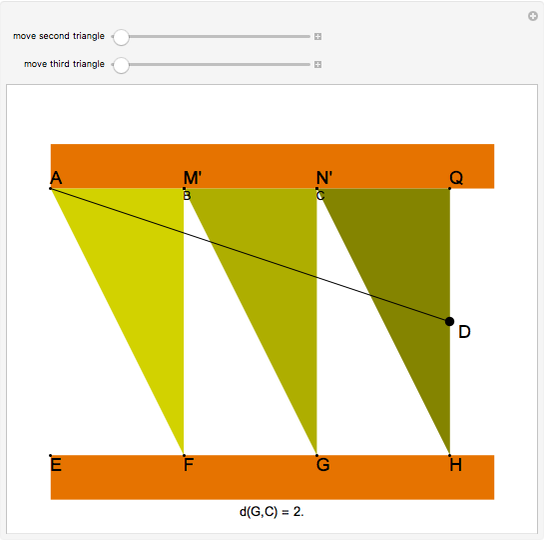
This Demonstration shows Eratosthenes's machine for finding two mean proportionals; that is, given lines and , find and such that . If and , the solution is . Let the lengths of and 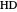be 2 and 1, respectively. Move the second and third triangles so that points 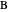and 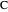lie on the straight line 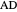, giving the length of as (approximately 1.25992…).

[more]

Eratosthenes's machine consists of a parallel frame and three congruent triangles. Let and . Move the triangles on the right so that and are on the line . By similarity .

[less]

Contributed by: Izidor Hafner (July 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The problem of doubling the cube was to find by ruler and compass, which was proved impossible [1]. This Demonstration shows a solution by sliding a line, which is not an allowable operation in a construction by ruler and compass.

Reference

[1] J. J. O'Connor and E. F. Robertson."Doubling the Cube." MacTutor History of Mathematics archive. (Jun 26, 2012) www-history.mcs.st-and.ac.uk/HistTopics/Doubling_the_cube.html.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send