Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

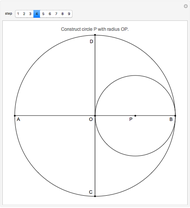
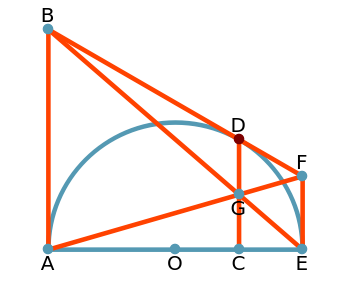The See-Saw Lemma

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

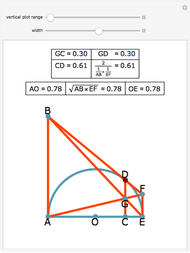
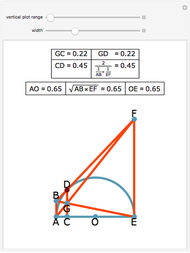
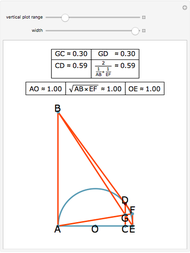
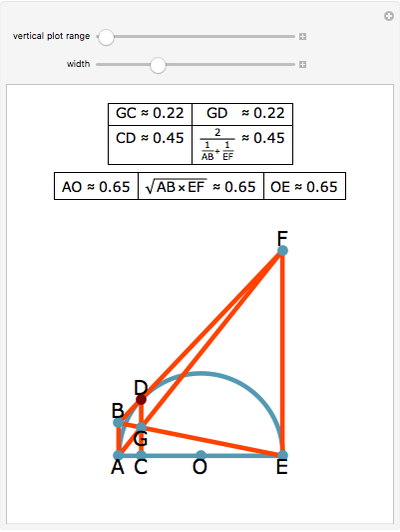
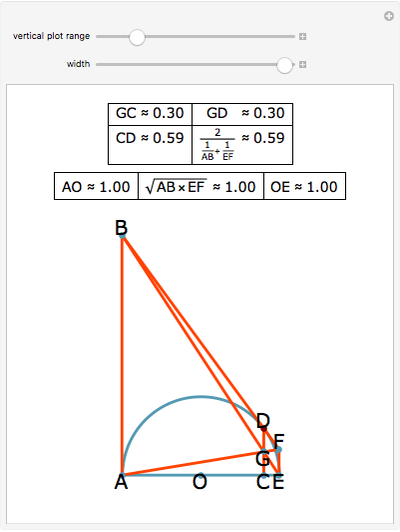
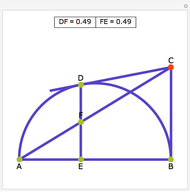
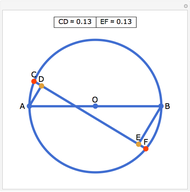
Draw a semicircle with base AE and center at O. Let the tangent line to the semicircle at D meet the perpendiculars drawn from A and E at B and F. Let G be the point of intersection of BE and AF. Let C be the projection of D onto AE. Then there are three results: (1) GC = GD, (2) CD is equal to the harmonic mean of AB and EF: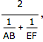 and (3) AO and OE equal the geometric mean of AB and EF: .

[more]

Drag the brown point or the sliders to change the figure.

[less]

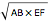Contributed by: Jay Warendorff (March 2011)
Based on work by: Alexander Bogomolny
Open content licensed under CC BY-NC-SA

Snapshots

Details

For more information see See-Saw Lemma: What Is This About?.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send