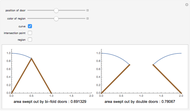
The Spatial Efficiency of the Bifold Door

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
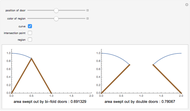
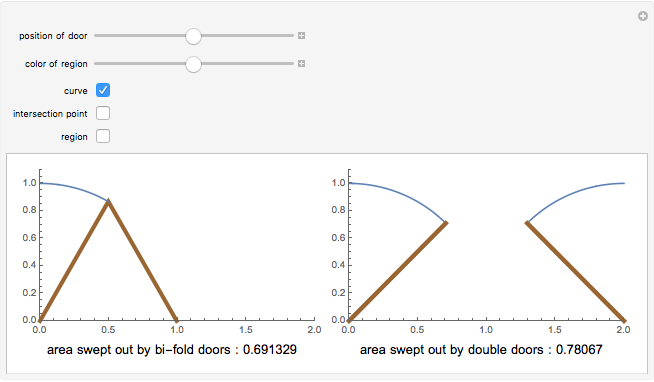
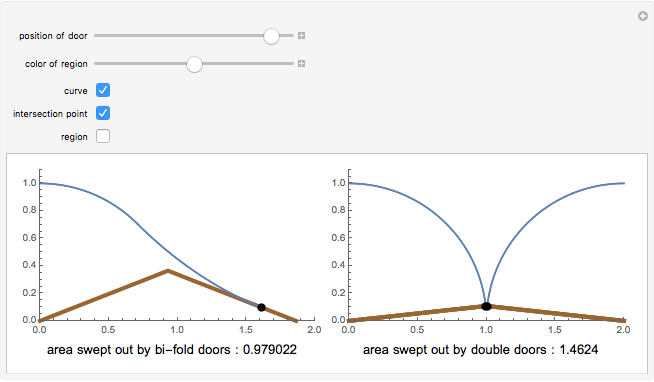
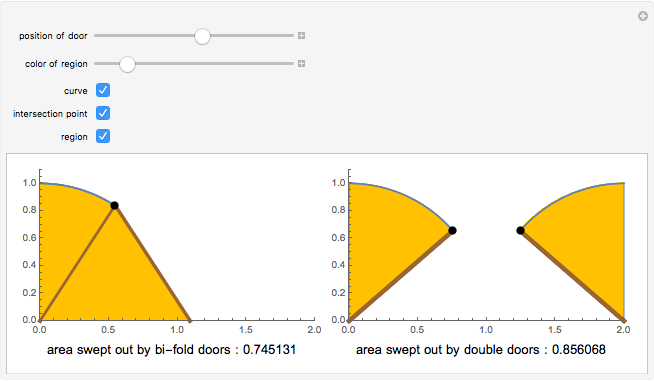
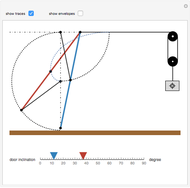
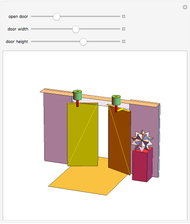
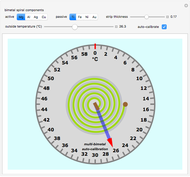
Consider the typical bifold door, often used for closets; as it opens, it sweeps out a region enclosed by a curve. The equation for the boundary curve of this region is 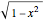 for
for 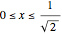 and
and 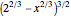 for
for 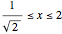 .
.
Contributed by: Matt Nicholson, Roshan Rajan, and Jennie Yang (June 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
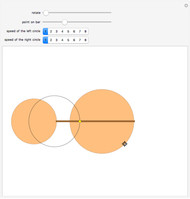
The problem of finding the equation for the boundary curve of an opening bifold door is very interesting. The door has two halves, each of length one, and goes from fully closed to fully open.
The boundary curve ends up being a piecewise function; the first part of the curve is determined by the point of the hinge, while the second part is determined by the edge of the second door, with that door being tangent to the second part of the curve at all times.
The first part of the curve is easy enough to find. The equation is 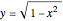 , which is just based on the equation of a circle.
, which is just based on the equation of a circle.
The second part of the curve is more demanding. We can find a way to quantify how much the door is open, then use a limit to find the point of intersection between the door and curve, which we can then use to find the actual equation of the curve.
Say that the  coordinate of the position of the door hinge is
coordinate of the position of the door hinge is  . Then, the
. Then, the 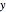 coordinate of the hinge is at
coordinate of the hinge is at 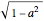 , since the edge of the first door just follows a circle.
, since the edge of the first door just follows a circle.
From this, we can determine that the equation of the line that follows the second door panel is 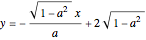 .
.
Then, suppose that we open the door slightly wider, such that the hinge point is at 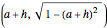 . Then the new equation for the door is
. Then the new equation for the door is 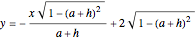 .
.
These two door positions, when the hinge is at  and when it is at
and when it is at  , intersect at
, intersect at 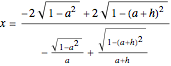 .
.
If we take the limit as  approaches 0, then we find the point at which the door intersects (and is tangent to) the curve. The limit of
approaches 0, then we find the point at which the door intersects (and is tangent to) the curve. The limit of  as
as  turns out to be
turns out to be 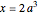 (or
(or  ). (This means that we can find the point of tangency with respect to the position of the door hinge with the equation
). (This means that we can find the point of tangency with respect to the position of the door hinge with the equation 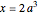 .)
.)
Now, we have an expression for the location of the tangent point based on the position of the door. Therefore, we can substitute this result into the original equation for the second door panel to get 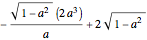 .
.
If we manipulate this expression a little, we get 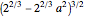 . Substituting
. Substituting  gives the equation of the second part of the curve,
gives the equation of the second part of the curve, 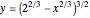 (an astroid).
(an astroid).
To find where the piecewise function changes from one part to the other, solve for when the two equations intersect. This occurs at  .
.
Therefore the equation of the curve is 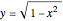 for
for 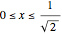 and
and 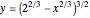 for
for 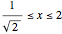 .
.
References
[1] T. Apostol and M. Mnatsakanian, "A New Look at the So-Called Trammel of Archimedes," The American Mathematics Monthly, 116(2), 2009 pp. 115–133.
[2] L. Riddle. "The Bi-Fold Door Problem." (Nov 1993) ecademy.agnesscott.edu/~lriddle/bidoor/solution.htm.
[3] D. Seiple, E. Boman, and R. Brazier, "Mom! There's an Astroid in My Closet!" Mathematics Magazine, 80(2), 2007 pp. 104–111.
[4] Mathematics Magazine, 66(3), 1993 p. 193.
Special thanks to the University of Illinois NetMath Program and the Mathematics department at William Fremd High School.
Permanent Citation