Sliding Along a Tautochrone Path

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
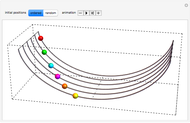
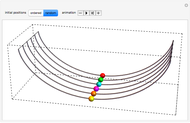
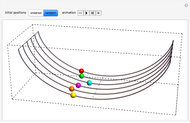
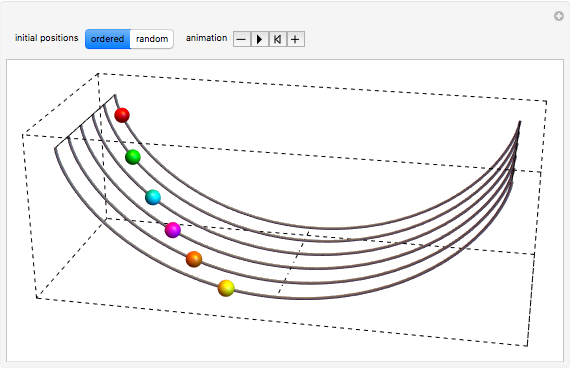
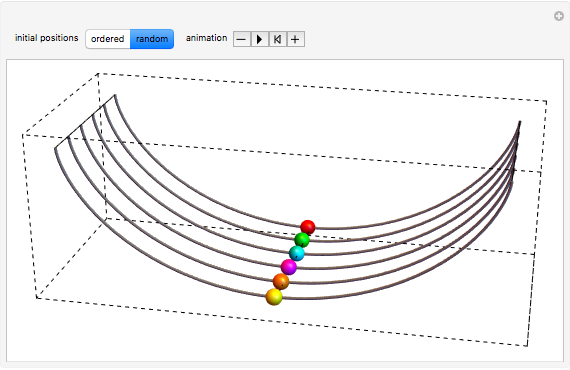
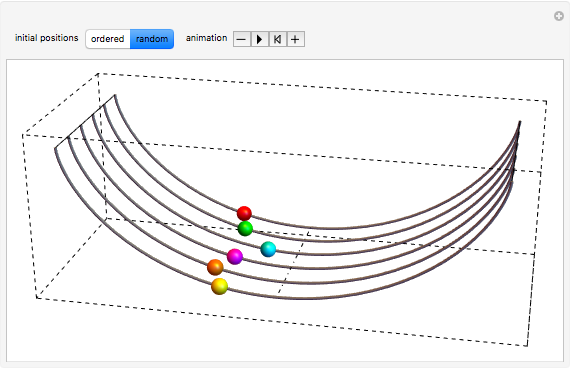
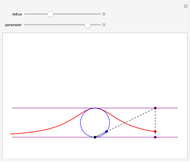
This Demonstration illustrates the fact that a cycloid is a tautochrone (isochronous) path. Six beads slide without friction down and up six cycloidal wire paths, starting from different positions and with zero initial speed. It can be seen that the six beads always reach the bottom simultaneously.
Contributed by: Erik Mahieu (November 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The tautochrone path is the cycloid formed by a circle of radius 1 rolling on the  axis from
axis from 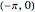 to
to 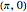 . With
. With 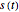 as the position of a bead at time
as the position of a bead at time  , this cycloid has the parametric equations
, this cycloid has the parametric equations 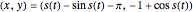 . Using Lagrangian dynamics, with
. Using Lagrangian dynamics, with 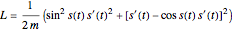 , the resulting equation of motion is
, the resulting equation of motion is  .
.
Permanent Citation
"Sliding Along a Tautochrone Path"
http://demonstrations.wolfram.com/SlidingAlongATautochronePath/
Wolfram Demonstrations Project
Published: November 30 2011