Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

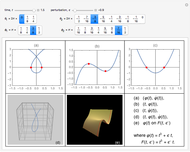
Time-Series Analysis for Generalized Logistic Maps with z-Unimodality

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

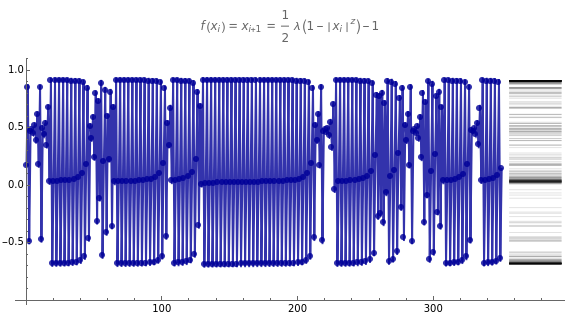
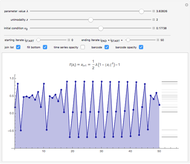
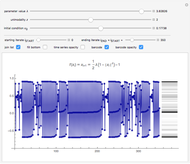
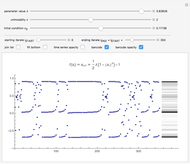
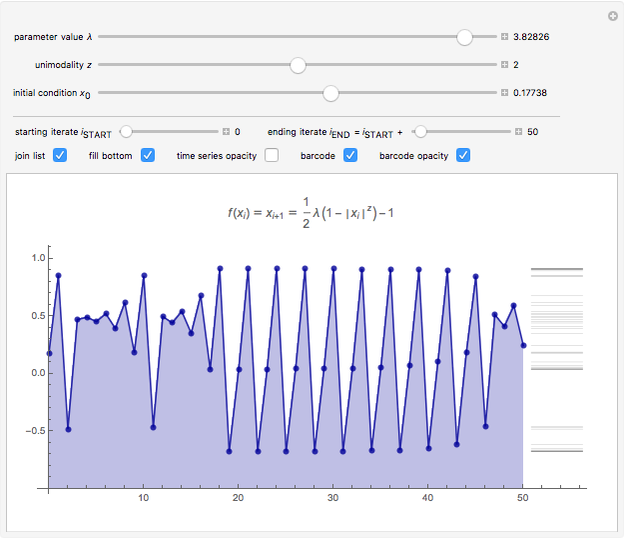
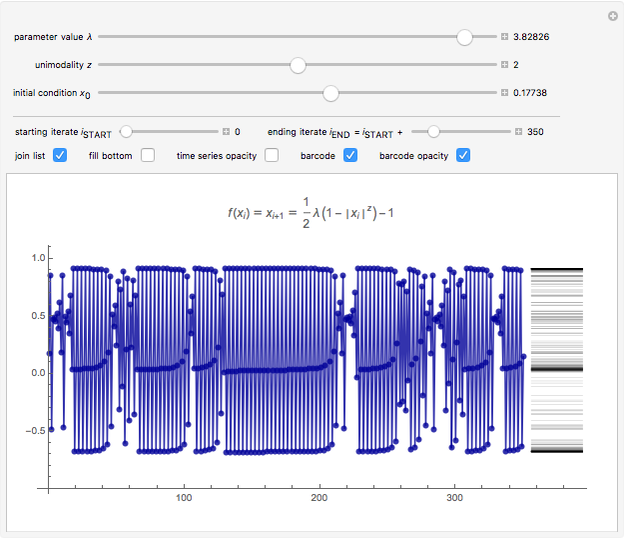
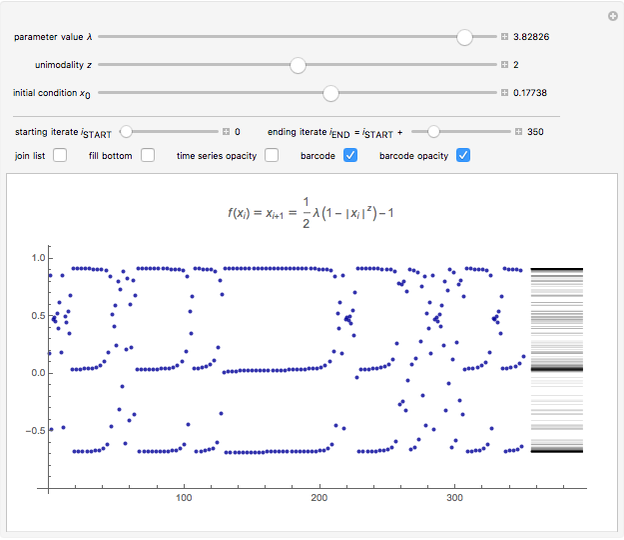
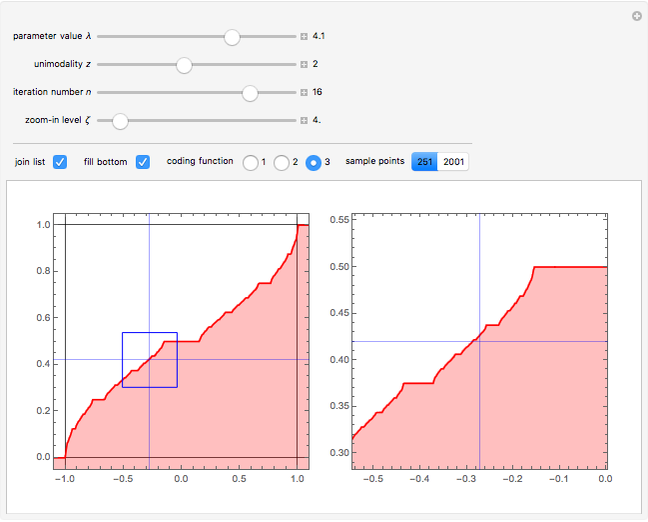
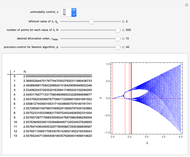
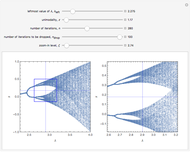
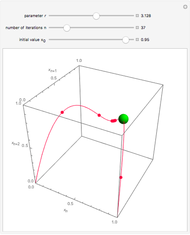
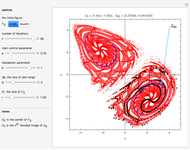
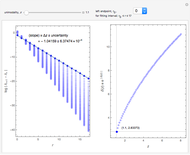
This Demonstration shows a time-series plot of an iterative map with a barcode attachment. The test map, , generalizes the well-known logistic map 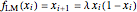[1–7]. Here is the iteration number, 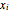is the iterate of 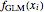starting from the initial value , 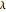is the main control parameter, and is the subcontrol parameter (which determines the unimodality, the degree of the local maximum of ).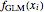

Contributed by: Ki-Jung Moon (December 2013)
Based on a program by: Stephen Wolfram
Open content licensed under CC BY-NC-SA

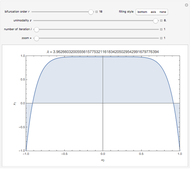
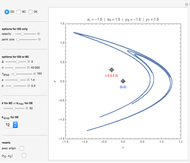
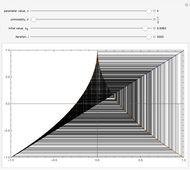
Snapshots

Details

References

[1] K. T. Alligood, T. D. Sauer, and J. A. Yorke, Chaos: An Introduction to Dynamical Systems, New York: Springer, 1996.

[2] S. H. Strogatz, Nonlinear Dynamics and Chaos, New York: Perseus Books Publishing, 1994.

[3] S. Wolfram, A New Kind of Science, Champaign, IL: Wolfram Media, 2002.

[4] K.-J. Moon, "Reducible Expansions and Related Sharp Crossovers in Feigenbaum's Renormalization Field," Chaos: An Interdisciplinary Journal of Nonlinear Science, 18, 2008 pp. 023104.

[5] K.-J. Moon, "Erratum: Reducible Expansions and Related Sharp Crossovers in Feigenbaum's Renormalization Field," Chaos: An Interdisciplinary Journal of Nonlinear Science, 20, 2010 pp. 049902.

[6] M. J. Feigenbaum, "Quantitative Universality for a Class of Non-Linear Transformations," Journal of Statistical Physics, 19, 1978 pp. 25–52.

[7] M. J. Feigenbaum, "The Universal Metric Properties of Nonlinear Transformations," Journal of Statistical Physics, 21, 1979 pp. 669–706.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send